数据结构
网络
关系型数据库管理系统(RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学临界角与折射率之间的关系
引言
折射率与临界角成正比。当光线从一种介质传播到另一种介质时，会产生临界角。这种角度的光线会照射到位于较低折射率介质和另一种介质之间的界面。此时，光线不会在第一种介质中反射。临界角的极限可以通过特定的公式来测量。
临界角的特征
该角度受折射率变化的强烈影响。
折射率可能从第一种介质到第二种介质发生变化。
光线的波长在改变角度的性质方面起着重要作用 (Shahsafi et al. 2018)。
对于较长的波长，临界角也会相应增加。
临界角和折射率的必要条件
| 组成部分 | 必要条件 |
| 临界角 | 入射角需要大于另一个角度。 光线需要从稠密介质移动到低密度介质。 |
| 折射率 | 光学基底的密度需要合适。 介质的温度需要适宜，以便折射率的值可以相应变化。 光线的波长需要成比例。 |
表1：临界角和折射率的重要条件
折射率的特征
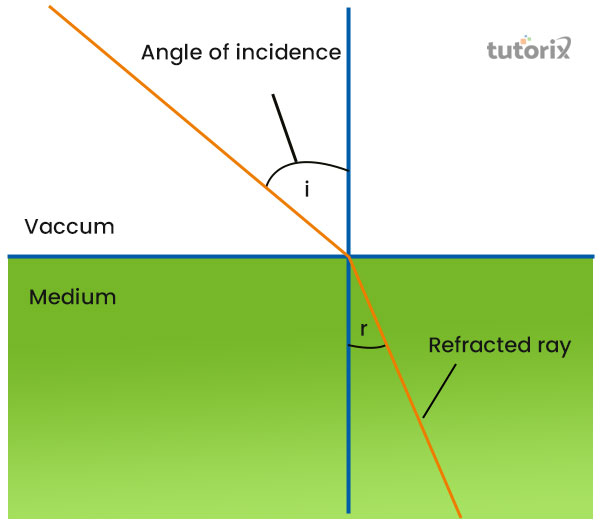
图1：折射率
折射率是一个重要的材料特性。
折射率有助于描述材料对光速的影响过程。
折射率主要用符号n表示 (Grebenikova et al. 2018)。
有时也使用符号μ来表示该折射率的值。
符号v代表光在材料中传播的速度。
临界角和折射率的应用
在日常生活中，折射率被广泛用于测量气体、固体和液体的值。折射率也用于测量溶质的浓度。一些使用者还发现它有助于区分宝石。
折射率具有显著且独特的变彩性 (Danny et al. 2019)。这些特性帮助用户正确区分各种宝石。与折射率相关的两个最重要的因素是介质的类型和性质。
折射率的值随介质的性质而变化。在真空介质中，折射率的值估计为1，而在氦气中，其值增加到1.000036 (Mammothmemory.net, 2022)。
水作为一种介质，在折射介质中的值为1.30。随着密度的增加，糖溶液和玻璃的值相应地从水的1.38增加到1.5 (Koutserimpas & Fleury, 2018)。
金刚石是密度最高的介质，其值为2.4。根据这些值，可以估计根据介质的变化而变化的折射率。
临界角被广泛用于制造光纤通信。在光空间滤波的情况下，临界角的应用也很重要 (Niskanen et al. 2019)。在现实生活中，临界角的知识非常重要且相关，因为它有助于理解反射发生的可能性。关于水-空气边界，临界角的值可以为48.6度。
关于玻璃-水边界，临界角的值估计为61.0度。临界角的一个重要的实际应用是其在收集电信号中的用途。计算机用户还使用临界角来传输信号 (Maurya et al. 2018)。这有助于电子设备保持连接，因为光线在改变传播介质时会改变方向。
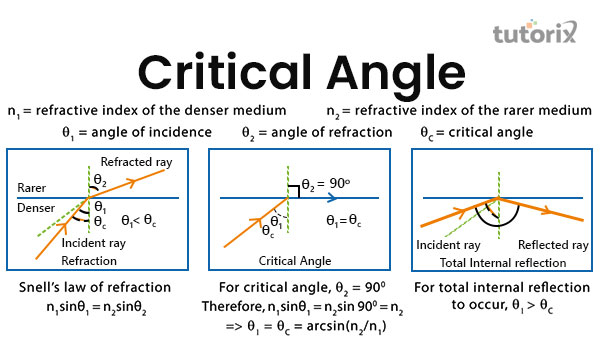
图2：临界角
临界角的SI单位是度，而折射率没有SI单位。应用斯涅尔定律是理解临界角和折射率变化的重要部分。
折射率和临界角的公式
该公式为θcrit = sin-1(nr/ni)。该公式的结果可以表示为sin-1(1/1.67) = 1.064rad。
该角度与入射角有关。当光线从密度较小的介质进入密度较大的介质时，其方向会发生变化 (Liu et al. 2019)。还发现光线会向法线方向弯曲。折射率 (n)= 1/(Sin C)
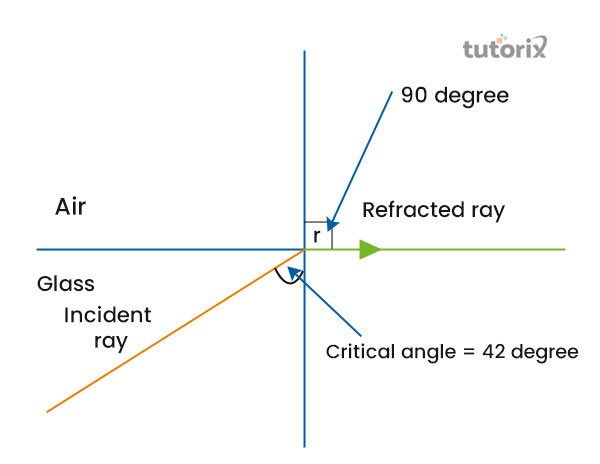
图3：折射率和临界角之间的关系
结论
推导折射率和临界角是一个重要的部分，以便可以分析这两个组成部分之间的关系。光的考虑与临界角的概念紧密相连。根据入射角的值，可以确定临界角的值。
常见问题
Q1. 临界角取决于哪些因素？
光的波长、折射率的值和介质温度是这些因素，临界角的值因这些因素而异。可以通过将临界角的特性应用于荧光显微镜来测量内反射。
Q2. 折射介质组分的指示符号是什么？
折射率的稠密介质用μb表示，用μa表示该折射率的稀疏介质。折射率的值为900，其中也包括稀疏介质的影响。
Q3. 折射率中的C代表什么？
折射率C代表光在真空中传播的速度。介质结构的物理条件也是一个重要部分。
Q4. 温度与临界角的关系是什么？
随着周围温度的升高，临界角的值也会增加。这种关系也会影响折射率的值。
参考文献
期刊
Danny, C. G., Raj, M. D., & Sai, V. V. R. (2019). Investigating the refractive index sensitivity of U-bent fiber optic sensors using ray optics. Journal of Lightwave Technology, 38(6), 1580-1588. Retrieved from: https://opg.optica.org
Grebenikova, N. M., Myazin, N. S., Rud, V. Y., & Davydov, R. V. (2018, October). Monitoring of flowing media state by refraction phenomenon. In 2018 IEEE International Conference on Electrical Engineering and Photonics (EExPolytech) (pp. 295-297). IEEE. Retrieved from: https://www.researchgate.net
Koutserimpas, T. T., & Fleury, R. (2018). Electromagnetic waves in a time-periodic medium with step-varying refractive index. IEEE Transactions on Antennas and Propagation, 66(10), 5300-5307. Retrieved from: https://ieeexplore.ieee.org
Liu, S., Deng, Z., Li, J., Wang, J., Huang, N., Cui, R., ... & Tian, J. (2019). Measurement of the refractive index of whole blood and its components for a continuous spectral region. Journal of biomedical optics, 24(3), 035003. Retrieved from: https://www.spiedigitallibrary.org
Maurya, J. B., François, A., & Prajapati, Y. K. (2018). Two-dimensional layered nanomaterial-based one-dimensional photonic crystal refractive index sensor. Sensors, 18(3), 857. Retrieved from: https://www.mdpi.com
Niskanen, I., Suopajärvi, T., Liimatainen, H., Fabritius, T., Heikkilä, R., & Thungström, G. (2019). Determining the complex refractive index of cellulose nanocrystals by the combination of Beer-Lambert and immersion matching methods. Journal of Quantitative Spectroscopy and Radiative Transfer, 235, 1-6. Retrieved from: http://jultika.oulu.fi
Shahsafi, A.，Xiao, Y.，Salman, J.，Gundlach, B. S.，Wan, C.，Roney, P. J. & Kats, M. A. (2018)。使用折射率低于1的电介质的中红外光学。应用物理评论，10(3), 034019。检索自：https://arxiv.org
网站
Mammothmemory.net (2022)。关于不同的折射率。检索自：https://mammothmemory.net [检索日期：2022年6月10日]
Sciencefacts.net (2022)。关于临界角。检索自：https://www.sciencefacts.net [检索日期：2022年6月10日]
浏览量：1000+
