数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学Python程序：查找子树节点值之和的最小值
假设我们有一棵树，其所有节点编号为1到n。每个节点包含一个整数值。现在，如果我们从树中移除一条边，则两棵子树的节点值之和的差必须最小。我们必须找出并返回此类子树之间最小的差值。树以边的集合形式提供给我们，节点的值也已提供。
因此，如果输入类似于n = 6，edge_list = [[1, 2], [1, 3], [2, 4], [3, 5], [3, 6]]，values = [15, 25, 15, 55, 15, 65]，则输出将为0。
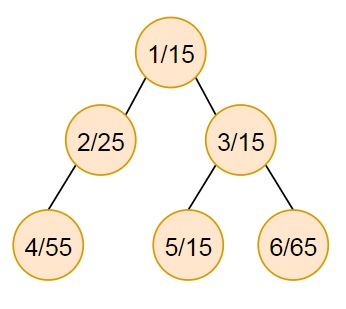
如果移除边(1,2)，则权重之和变为80, 110。差值为30。
如果移除边(1,3)，则权重之和变为95, 95。差值为0。
如果移除边(2,4)，则权重之和变为55, 135。差值为80。
如果移除边(3,5)，则权重之和变为15, 175。差值为160。
如果移除边(3,6)，则权重之和变为65, 125。差值为60。
所以最小权重为0。
为了解决这个问题，我们将遵循以下步骤：
- adj_list := 一个大小为n的新列表，包含空列表
- 对于edge_list中的每条边，执行：
- u := edge[0]
- v := edge[1]
- 在adj_list[u-1]的末尾插入v-1
- 在adj_list[v-1]的末尾插入u-1
- value_list := 一个大小为n的新列表，初始化为0
- not_visited := 一个大小为i的新映射，其中i是adj_list中非空列表的数量
- 当not_visited不为空时，执行：
- 对于not_visited中的每个i，执行：
- value_list[i] := value_list[i] + values[i]
- 如果adj_list[i]的长度非零，则
- 从adj_list[adj_list[i, 0]]中删除i
- value_list[adj_list[i, 0]] := value_list[adj_list[i, 0]] + value_list[i]
- 对于not_visited中的每个i，执行：
- 如果len(adj_list[i]) 和 len(adj_list[adj_list[i, 0]]) == 1，则
- not_visited := 一个包含adj_list[i, 0]的新列表
- 如果len(adj_list[i]) 和 len(adj_list[adj_list[i, 0]]) == 1，则
- 对于not_visited中的每个i，执行：
- return_val := |sum(values) - 2 * value_list[0]|
- 对于从1到n的i，执行：
- decision_val := |sum(values) - 2 * value_list[i]|
- 如果decision_val < return_val，则
- return_val := decision_val
- 返回return_val
示例
让我们看看下面的实现以更好地理解：
def solve(n, edge_list, values):
adj_list = [[] for i in range(n)]
for edge in edge_list:
u = edge[0]
v = edge[1]
adj_list[u-1].append(v-1)
adj_list[v-1].append(u-1)
value_list = [0] * n
not_visited = {i for i in range(n) if len(adj_list[i]) == 1}
while(len(not_visited)):
for i in not_visited:
value_list[i] += values[i]
if(len(adj_list[i])):
adj_list[adj_list[i][0]].remove(i)
value_list[adj_list[i][0]] += value_list[i]
not_visited = {adj_list[i][0] for i in not_visited if
len(adj_list[i]) and len(adj_list[adj_list[i][0]]) == 1}
return_val = abs(sum(values) - 2 * value_list[0])
for i in range(1, n):
decision_val = abs(sum(values) - 2 * value_list[i])
if decision_val < return_val:
return_val = decision_val
return return_val
print(solve(6, [[1, 2], [1, 3], [2, 4], [3, 5], [3, 6]], [10, 20, 10, 50, 10, 60]))输入
6, [[1, 2], [1, 3], [2, 4], [3, 5], [3, 6]], [10, 20, 10, 50, 10, 60]
输出
0
更新于：2021年10月23日
浏览量：121
广告