查找图中两顶点之间惩罚值最小的路径的程序（Python）

假设我们给定一个无向加权图，并要求找出从节点 a 到节点 b 惩罚值最小的路径。路径的惩罚值是路径中所有边的权重的按位或结果。因此，我们必须找出这样的“最小惩罚值”路径，如果两个节点之间不存在路径，则返回 -1。

例如，输入为：

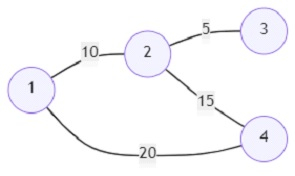
起点 (s) = 1，终点 (e) = 3；则输出为 15。

顶点 1 和 3 之间存在两条路径。最佳路径是 1->2->3，路径代价为 (10 或 5) = 15。

为了解决这个问题，我们将遵循以下步骤：

  • 定义一个函数 helper()。它将接收 G、s、e 作为参数。
    • v := 一个新的集合
    • c := 一个大小为 n 的新列表，初始化值为无穷大
    • heap := 一个新的堆，包含 (0, s) 对
    • 当堆的大小 > 0 时，执行以下操作：
      • cst := 从堆中弹出最小项
      • cur := 从堆中弹出最小项
      • c[cur] := min(cst, c[cur])
      • 如果 (cst, cur) 存在于 v 中，则
        • 进行下一次迭代
      • 如果 cur 等于 e，则
        • 返回 c[cur]
      • 将 (cst, cur) 对添加到 v
      • 对于 G[cur] 中的每个邻居 n_cost，执行以下操作：
        • 将 ((n_cost 或 cst), neighbor) 推入堆
    • 返回 c[e]
  • G := 包含 n+1 个空列表的新列表
  • 对于 edges 中的每一项，执行以下操作：
    • u := item[0]
    • v := item[1]
    • w := item[2]
    • 将 (v, w) 对插入到 G[u] 的末尾
    • 将 (u, w) 对插入到 G[v] 的末尾
  • ans := helper(G, s, e)
  • 如果 ans 等于无穷大，则返回 -1，否则返回 ans

示例

让我们看看下面的实现，以便更好地理解：

import heapq
from math import inf

def helper(G, s, e):
    v = set()
    c = [inf] * len(G)
    heap = [(0, s)]
    while len(heap) > 0:
        cst, cur = heapq.heappop(heap)
        c[cur] = min(cst, c[cur])
        if (cst, cur) in v:
            continue
        if cur == e:
            return c[cur]
        v.add((cst, cur))
        for neighbor, n_cost in G[cur]:
            heapq.heappush(heap, (n_cost | cst, neighbor))
    return c[e]

def solve(n, edges, s, e):
    G = [[] for _ in range(n + 1)]
    for item in edges:
        u, v, w = map(int, item)
        G[u].append((v, w))
        G[v].append((u, w))
    ans = helper(G, s, e)
    return -1 if ans == inf else ans

print(solve(4, [(1, 2, 10), (2, 3, 5), (2, 4, 15), (1, 4, 20)], 1, 3))

输入

4, [(1, 2, 10), (2, 3, 5), (2, 4, 15), (1, 4, 20)], 1, 3

输出

15

更新于：2021年10月6日

318 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告