C++程序：查找给定圆形两部分角度的最小差值

---

在本文中，我们将使用C++编程语言查找给定圆形两部分之间角度的最小差值。在继续编写代码之前，让我们先了解如何计算角度以找到它们之间的最小差值。

给定数组中圆形所有部分的角度。我们必须以角度差值最小的方式连接这些部分。

让我们通过输入和输出场景来更好地理解。在这里，我们声明一个数组，其中包含如下所示的圆形的三个不同角度：

输入

 ang[] = {160, 120, 80}

输出

 40

解释

在这个输入和输出场景中，给定三个部分的角度：120°、80°和160°，我们想要连接其中的两个部分以形成角度差值最小的扇区。

步骤1：我们可以选择120°和80°的部分。两个角度之和是120°和80°，总计为（120 + 80 = 200）。

步骤2：组合角度与剩余部分（160°）之间的差值为：[ |(120° + 80°) - 160°| = |200° - 160°| = 40° ]

以下是我们绘制角度的圆形图：

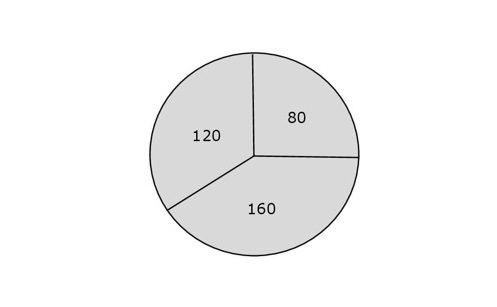
解决方案方法

在这里，我们必须合并所有部分以构成两部分。为此，我们需要取连续的部分（例如，我们不能将ang1和ang3放在一起）。

让我们取部分1的角度为A。

那么部分2的角度将为360 - A。

差值为|A - (360 - A)|。我们取绝对值，因为只能有正角度。

解差值方程：

2 * |A - 180|，这需要是最小值。为此，我们将尝试合并圆形的所有可能部分，并找到(2*|A - 180|)的最小值。

示例

以下是使用C++查找给定圆形两部分角度最小差值的程序：

#include <iostream>
#include <math.h>
using namespace std;
int CalcSmallDiffAng(int ang[], int n) {
   int Left = 0, A = 0, minDiff = 360;
   for (int i = 0; i < n; i++) {
      A += ang[i];
      while (A >= 180) {
         minDiff = min(minDiff, 2 * abs(180 - A));
         A -= ang[Left];
         Left++;
      }
      minDiff = min(minDiff, 2 * abs(180 - A));
   }
   return minDiff;
}
int main() {
   int ang[] = { 160, 120, 80 };
   int n = sizeof(ang) / sizeof(ang[0]);
   cout<<"The smallest difference of angles of two parts of a given circle is "<<CalcSmallDiffAng(ang, n);
   return 0;
}

输出

上述程序显示以下输出：

The smallest difference of angles of two parts of a given circle is 40