Python程序重置多边形到初始状态

假设，有一个具有n个顶点、n个翻转轴和n个旋转点的多边形。以下关于翻转轴和旋转点是正确的

  • 如果n是奇数，每个翻转轴都只穿过一个顶点和相对边的中点。
  • 如果n是偶数，一半的轴穿过一对相对顶点，另一半穿过一对相对边。
  • 连续两个轴之间的角度为360/2n。

现在，我们旋转给定的多边形。我们有n种不同类型的旋转器，k-旋转器将多边形绕第k个轴顺时针旋转(360 x k)/n度。有一个输入列表，其中包含若干对整数。每对整数中的第一个整数表示多边形是翻转还是旋转。如果第一个整数是1，则多边形被旋转，如果它是2，则多边形被翻转。第二个整数是k，如果多边形被翻转，则它在第k个轴上被翻转；否则，如果它被旋转，则它被旋转360/2n度。然后在列表不为空时执行旋转和翻转。

我们这里需要做的就是在列表中添加另一个元素，以便将多边形重置到其初始位置。

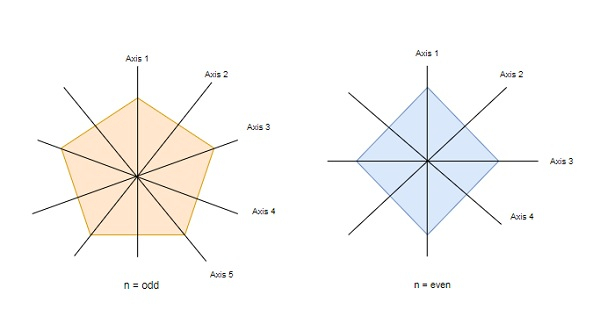
图像指定了两种类型多边形的旋转轴。

所以，如果输入类似于n = 6，input_list = [[1, 2], [1, 4], [2, 3], [2, 5], [1, 6]]，则输出将是(1, 4)

在进行变换后，沿着第4个轴进行旋转将使多边形重置到其初始位置。

为了解决这个问题，我们将遵循以下步骤：

  • decision_var := False
  • position := 0
  • 对于input_list中的每个项目，执行以下操作
    • x := item[0]
    • y := item[1]
    • 如果x等于1，则
      • position := position + y
    • 否则
      • position := y - position
      • decision_var := not(decision_var)
  • position := position mod n
  • 如果decision_var不为零，则
    • 返回一对(2, position)
  • 否则，
    • 返回一对(1, n - position)

示例

让我们看看以下实现以更好地理解：

def solve(n, input_list):
   decision_var = False
   position = 0

   for item in input_list:
      x = item[0]
      y = item[1]
      if x == 1:
         position += y
      else:
         position = y - position
         decision_var = not decision_var
   position = position % n

   if decision_var:
      return (2, position)
   else:
      return (1, n - position)

print(solve(6, [[1, 2], [1, 4], [2, 3], [2, 5], [1, 6]]))

输入

6, [[1, 2], [1, 4], [2, 3], [2, 5], [1, 6]]

输出

(1, 4)

更新于： 2021年10月23日

131 次查看

启动你的 职业生涯

通过完成课程获得认证

开始学习
广告