数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律Python程序：根据极角排序笛卡尔点集
假设我们有一个名为points的列表，其中包含一组笛卡尔点。我们需要根据它们的极角对它们进行排序。极角的范围在0到2*PI之间。如果一些点的极角相同，则根据该点到原点的距离对其进行排列。
因此，如果输入类似于points = [(1,1), (1,-2),(-2,2),(5,4),(4,5),(2,3),(-3,4)]，
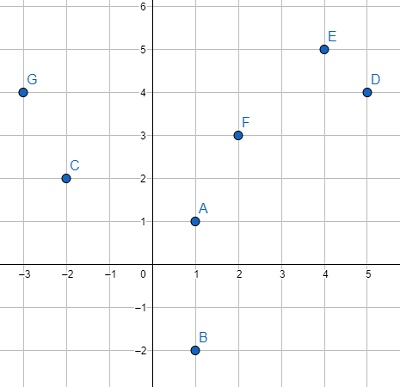
则输出将为[(5, 4), (1, 1), (4, 5), (2, 3), (-3, 4), (-2, 2), (1, -2)]
为了解决这个问题，我们将遵循以下步骤：
- 定义一个比较函数key()。它将接收x
- atan := x[1]/x[0] 的反正切
- 如果atan >= 0，则返回(atan, x[1]^2+x[0]^2)，否则返回(2*pi + atan, x[0]^2+x[1]^2)
- 然后使用比较函数key()对points进行排序
示例
让我们看看下面的实现来更好地理解：
import math def solve(points): def key(x): atan = math.atan2(x[1], x[0]) return (atan, x[1]**2+x[0]**2) if atan >= 0 else (2*math.pi + atan, x[0]**2+x[1]**2) return sorted(points, key=key) points = [(1,1), (1,-2),(-2,2),(5,4),(4,5),(2,3),(-3,4)] print(solve(points))
输入
[(1,1), (1,-2),(-2,2),(5,4),(4,5),(2,3),(-3,4)]
输出
[(5, 4), (1, 1), (4, 5), (2, 3), (-3, 4), (-2, 2), (1, -2)]
更新于: 2021年10月11日
1K+ 次查看
广告