矩形的性质

简介

在日常生活中，我们遇到各种由直线段围成的几何图形。这些被称为多边形。根据边数和角数，多边形被分为各种类型。矩形是欧几里得几何学中广泛使用的一种多边形。各种物体，如黑板、撞球板、书籍、门、智能手机、床等，都是矩形的现实例子。在本教程中，我们将讨论与矩形相关的含义、性质、类型和基本公式，并提供一些解题示例。

矩形

矩形是由四条直线段构成的二维多边形。换句话说，它被定义为具有四条边和四个角的四边形。它也是一个等角四边形，有两对平行的等边。此外，每个角的度数都是90°。“矩形”一词源于拉丁语“rectus”（意为“直的”或“正确的”）和“angulus”（意为“角”）。矩形的较长边称为长，较短边称为宽。此外，它还有两条对角线，如PR和QS。为了说明目的，下面表示一个矩形PQRS。

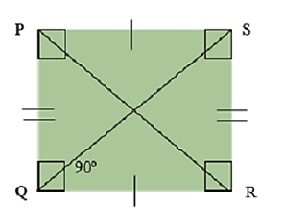
矩形的性质

这些性质帮助我们从其他几何构造中识别和识别矩形。矩形有几个性质，下面简要总结。

矩形是一个具有四条边和四个角的四边形。
对边平行且相等。
每个角的度数为90°。
矩形内角和为360°。
对角线的长度相等。
对角线互相平分。
矩形可以称为平行四边形。
可以使用勾股定理计算对角线的长度。如果长和宽分别为p和q，则对角线的长度将为$\mathrm{\sqrt{p^2+q^2}}$。
如果对角线互相垂直，则矩形称为正方形。

矩形的公式

矩形的公式有助于求面积和周长。让我们考虑一个长和宽分别为p和q的矩形。现在，可以使用以下公式确定矩形的面积和周长。

矩形的面积 = p×q
矩形的周长 = 2(p+q)

现实生活中的矩形

我们在日常生活中看到各种矩形的现实例子。其中一些如下所示。

示例	描述	图片
笔记本电脑	它看起来像一个具有相等平行对边的四边形。
书籍	虽然书籍是长方体形状；但是书籍的每个面都是一个矩形。
智能手机	智能手机的顶部和底部表面是矩形形状。
门	房门是矩形的常见例子。
巧克力	条形巧克力是矩形形状。
桌面	餐桌或学习桌是矩形形状。
床	单人床是矩形的一个例子。
黑板	黑板有一个矩形的面。
尺子	这种几何工具具有矩形结构。
信封	它具有扁平的矩形形状。
纸币	纸币也是矩形形状的。
借记卡或信用卡	塑料卡的形状是矩形。