数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济
心理学
社会科学
时装科学
法律科学Python 程序用于计算第 n 项斐波那契数
在本文中，我们将计算第 n 项斐波那契数。
斐波那契数由以下递归关系定义：
Fn = Fn-1 + Fn-2
其中 F0 = 0，F1 = 1。
前几个斐波那契数为
0,1,1,2,3,5,8,13,..................
我们可以使用递归法和动态规划法来计算斐波那契数。
现在让我们看看 Python 脚本形式的实现
方法 1：递归法
示例
#recursive approach
def Fibonacci(n):
if n<0:
print("Fibbonacci can't be computed")
# First Fibonacci number
elif n==1:
return 0
# Second Fibonacci number
elif n==2:
return 1
else:
return Fibonacci(n-1)+Fibonacci(n-2)
# main
n=10
print(Fibonacci(n))输出
34
下面显示了声明的所有变量的范围。
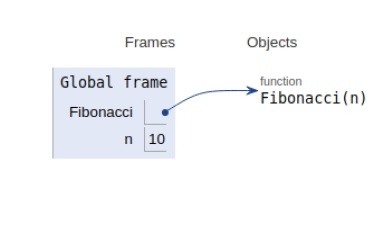
方法 2：动态规划法
示例
#dynamic approach
Fib_Array = [0,1]
def fibonacci(n):
if n<0:
print("Fibbonacci can't be computed")
elif n<=len(Fib_Array):
return Fib_Array[n-1]
else:
temp = fibonacci(n-1)+fibonacci(n-2)
Fib_Array.append(temp)
return temp
# Driver Program
n=10
print(fibonacci(n))输出
34
下面显示了声明的所有变量的范围
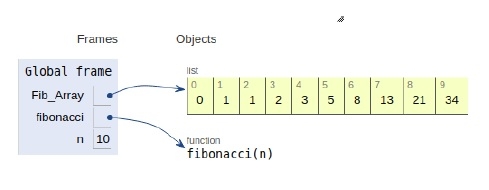
结论
在本文中，我们学习了使用递归法和动态规划法计算第 n 项斐波那契数。
更新日期：11-9-2019
1K+ 查看次数
广告