Python程序：求一个数的唯一质因数的乘积

在这篇文章中，我们将学习以下问题的解决方案：

问题陈述 - 给定一个数字 n，我们需要找到所有唯一质因数的乘积并返回它。

例如，

Input: num = 11
Output: Product is 11
Explanation:
Here, the input number is 11 having only 1 prime factor and it is 11.
And hence their product is 11.

方法 1

使用 for 循环，从 i = 2 到 n+1，检查 i 是否是 n 的因数，然后检查 i 本身是否为质数，如果是，则将乘积存储在 product 变量中，并继续此过程，直到 I 等于 n。

示例

 在线演示

def productPrimeFactors(n):
   product = 1
   for i in range(2, n+1):
      if (n % i == 0):
         isPrime = 1
         for j in range(2, int(i/2 + 1)):
            if (i % j == 0):
               isPrime = 0
               break
         if (isPrime):
            product = product * i
   return product
# main
n = 18
print (productPrimeFactors(n))

输出

6

所有变量的作用域如下图所示：

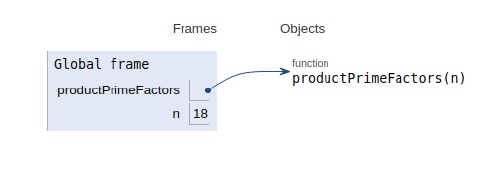
方法 2

  • 当 n 可以被 2 整除（偶数）时，打印 2 并将 n 除以 2。

  • 步骤 1 之后，n 必须变成奇数。现在从 i = 3 开始一个 for 循环，直到 n 的平方根。当 I 可以整除 n 时，打印 I 并将 n 除以 i。当 I 不能整除 n 时，将 I 加 2 并继续此过程。

  • 如果 n 是一个质数且大于 2，则通过上述两个步骤，n 不会变成 1。因此，如果 n 大于 2，则打印 n。

示例

import math
def productPrimeFactors(n):
   product = 1
   # prime factor 2
   if (n % 2 == 0):
      product *= 2
      while (n%2 == 0):
         n = n/2
# n must be odd
for i in range (3, int(math.sqrt(n)), 2):
   # While i divides n, print i and
   # divide n
   if (n % i == 0):
      product = product * i
      while (n%i == 0):
         n = n/i
   # n is a prime number greater than 2
   if (n > 2):
      product = product * n
   return product
# main()
n = 8
print (int(productPrimeFactors(n)))

输出

2

变量的作用域在下面的图像中说明：

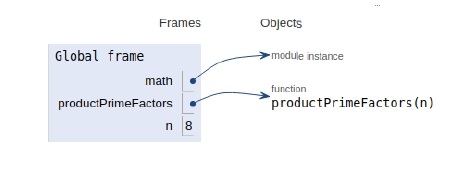
结论

在这篇文章中，我们学习了如何使用蛮力方法和高效方法来求解给定数字的唯一质因数的乘积。

更新于： 2019年9月11日

1K+ 次查看

开启你的 职业生涯

通过完成课程获得认证

立即开始
广告