四分位数

---

介绍

在统计学中，三个主要术语用于描述数据的集中趋势，即平均数、中位数和众数。但是，这些术语指的是代表中心值的特定数字。然而，四分位数是另一个统计术语，用于比上述术语更有效地描述数据。四分位数的概念通常用于比较一家公司的的数据与另一家公司的的数据。此外，它还用于以图形方式表示中位数和四分位数。在本教程中，我们将学习关于四分位数的定义、公式、偏差、范围以及一些相关的解题示例。

定义

四分位数定义为一种分位数类别，它将一个组分成四个部分或四分之一。分位数是将连续分布分成相等概率的切割点。它们是一种百分位数。四分位数有三个点，例如第一（Q₁）、第二（Q₂）和第三（Q₃）四分位数。此外，第二四分位数（Q₂）是其余两个四分位数的中位数。为了找到数据集的四分位数，需要将数据按升序排列。

公式

存在用于确定数据集四分位数的公式。使用公式，我们可以确定第一（位于第一项和中位数之间）、第二（中位数）和第三四分位数（位于中位数和最后一项之间）。在计算之前，应将数据集按升序排列。计算给定数据集四分位数的公式如下：

• 第一四分位数（Q₁）或下四分位数：$\mathrm{(\frac{m+1}{4})^{th}}$ 项

• 第二四分位数（Q₂）或四分位间距：$\mathrm{(\frac{m+1}{2})^{th}}$ 项

• 第三四分位数（Q₃）或上四分位数：$\mathrm{(\frac{3(m+1)}{4})^{th}}$ 项

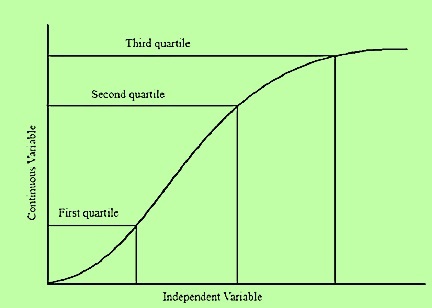
统计学中的四分位数

我们已经看到，四分位数将组分成四个部分。每个部分都位于特定范围内。因此，每个四分位数的范围如下所述。

符号	四分位数名称	范围
Q1	第一或下四分位数	将最低的 25% 与整个数据分开
Q2	第二四分位数或中位数	位于中位数值上，这意味着它将数据分成两半
Q3	第三或上四分位数	将最高的 25% 与整个数据分开

四分位差

它被定义为一种统计度量，它使用平均值来评估数据的偏差。换句话说，它确定了数据的平均值。它说明了分布的散布情况。它也称为**半四分位间距**。在数学上，它可以表示为：

四分位差 $\mathrm{= \frac{Q_3-Q_1}{2}}$

其中 Q₃-Q₁ 是四分位间距。

四分位差可以针对分组数据和非分组数据确定。让我们讨论评估四分位差的过程。

• 第一步，对于分组数据和非分组数据，都将数据按升序排列。

• 使用以下公式评估第一四分位数：

  非分组数据：$\mathrm{(Q_1) (\frac{m+1}{4})^{th}}$ 项

  分组数据： $\mathrm{Q_1=p_1+\frac{\frac{N}{4}-c}{f}(p_2-p_1)}$

  其中 m 是四分位数的数量。此外，p₁ 和 p₂ 是数据的下限和上限。N、f 和 c 分别是总频数、特定类别的频数和累积频数。

• 使用以下公式查找第三四分位数：

  非分组数据： $\mathrm{(Q_3) \:\: (\frac{3(m+1)}{4})^{th}}$ 项

  分组数据： $\mathrm{Q_3=p_1+\frac{\frac{3N}{4}-c}{f}(p_2-p_1)}$

• 现在，我们可以使用公式确定四分位差，如下所示：

  四分位差 = $\mathrm{= \frac{Q_3-Q_1}{2}}$

四分位间距

四分位间距是第一四分位数和第三四分位数之间的差。它衡量数据的散布情况，这意味着它衡量数据集中间 50% 的数据。

评估四分位间距的数学表达式为：

$$\mathrm{四分位间距 = Q_3-Q_1=(\frac{3(m+1)}{4})^{th} 项-(\frac{(m+1)}{4})^{th} 项 }$$

让我们讨论评估四分位间距的过程。

• 步骤 1：对于分组数据和非分组数据，都将数据按升序排列。

• 步骤 2：使用以下公式查找数据集的中位数（Q₂）。

  对于偶数数据集： $\mathrm{Q_2=\frac{(\frac{n}{2})^{th} 项+(\frac{n}{2}+1)^{th} 项}{2}}$

  对于奇数数据集： $\mathrm{Q_2=(\frac{n+1}{2})^{th} 项}$

• 步骤 3：查找四分位数 Q₁，它是步骤 2 中找到的中位数左侧数据点的中位数。

• 步骤 4：查找四分位数 Q₃，它是步骤 2 中找到的中位数右侧数据点的中位数。

  四分位间距 = Q₃-Q₁

解题示例

示例 1

评估以下数据集的中位数、下四分位数、上四分位数和四分位间距：

23, 56, 110, 12, 6, 89, 103

我们必须将数据集按升序排列，如下所示：

6, 12, 23, 56, 89, 103, 110

由于元素的数量为奇数（即 7），因此中位数 $\mathrm{=(\frac{7+1}{2})^{th} 项=12}$

第一四分位数（Q₁）或下四分位数：=$\mathrm{(\frac{m+1}{4})^{th} 项=(\frac{7+1}{4})^{th} 项=56}$

第三四分位数（Q₃）或上四分位数： $\mathrm{(\frac{3(m+1)}{4})^{th} 项=(\frac{3(7+1)}{4})^{th} 项=89}$

四分位间距 =Q₃-Q₁=89-56=33

∴ 以下数据集的中位数、下四分位数、上四分位数和四分位间距分别为 12、56、89 和 33。

示例 2

查找以下数据集的四分位差和四分位间距：

8, 20, 5, 16, 49, 32, 78, 56, 11, 39, 1

解答

我们必须将数据集按升序排列，如下所示：

1, 5, 8, 11, 16, 20, 32, 39, 49, 56, 78

由于元素的数量为奇数（即 11），因此中位数 =$\mathrm{(\frac{11+1}{2})^{th} 项= 32}$

第一四分位数（Q_1）或下四分位数：=$\mathrm{(\frac{m+1}{4})^{th} 项=(\frac{11+1}{4})^{th} 项=5}$

第三四分位数（Q_3）或上四分位数： $\mathrm{(\frac{3(11+1)}{4})^{th} 项=(\frac{3(11+1)}{4})^{th} 项=11}$

四分位差 $\mathrm{= \frac{Q_3-Q_1}{2}=\frac{11-5}{2}=3 }$

现在，四分位间距 $\mathrm{=Q_3-Q_1=11-5=6}$

∴ 数据集的四分位差和四分位间距分别为 3 和 6。

结论

本教程简要介绍了四分位数及其在统计学中的应用。此外，还说明了与四分位差和四分位间距相关的基本公式。此外，还提供了一些解题示例，以便更好地理解这个概念。总之，本教程可能有助于理解四分位数的基本概念。

常见问题

1. 如何确定四分位差系数？

四分位差系数可以使用以下表达式确定 $\mathrm{\frac{Q_3-Q_1}{Q_3+Q_1}}$。

2. 标准差和四分位差有什么区别？

当给出极端异常值时，标准差用于测量数据的离散程度。如果没有提供极端异常值，则应使用四分位差来确定数据的分布散布。

3. 四分位数有哪些应用？

四分位数是一种统计工具，用于创建数据集的箱线图。此外，它有助于比较一家公司的的数据与另一家公司的的数据。

4. 哪个四分位数被称为数据集的中位数？

第二四分位数是数据集的中位数。

5. 哪个区域属于第一四分位数？

第一四分位数将数据集的前 25% 与后 75% 分开。