数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究C++ 中无符号整数的恢复除法算法
讨论使用除法算法对无符号整数进行除法。一些除法算法应用于纸上，另一些则在数字电路中实现。除法算法分为两种类型：慢速除法算法和快速除法算法。慢速除法算法包括恢复、非恢复、SRT 和非恢复算法。
在本教程中，我们将讨论恢复算法，假设 0 < 除数 < 被除数。
求解方法
在这里，我们将使用寄存器 Q 存储商，寄存器 A 存储余数，M 存储除数。A 的初始值保持为 0，并且其值被恢复，这就是这种方法被称为恢复除法的原因。
用值初始化寄存器，
Q = 被除数，
A = 0，
M = 除数，
N = 被除数的位数。
AQ 左移意味着将寄存器 A 和 Q 作为一个单元。
用 A 减去 M 并存储在 A 中。
检查 A 的最高有效位
如果为 0，则将最低有效位设置为 1。
否则，将最低有效位设置为 0。
恢复 A 的值并递减计数器 N 的值。
如果 N = 0，则退出循环；否则，转到步骤 2。
商存储在寄存器 Q 中。
流程图
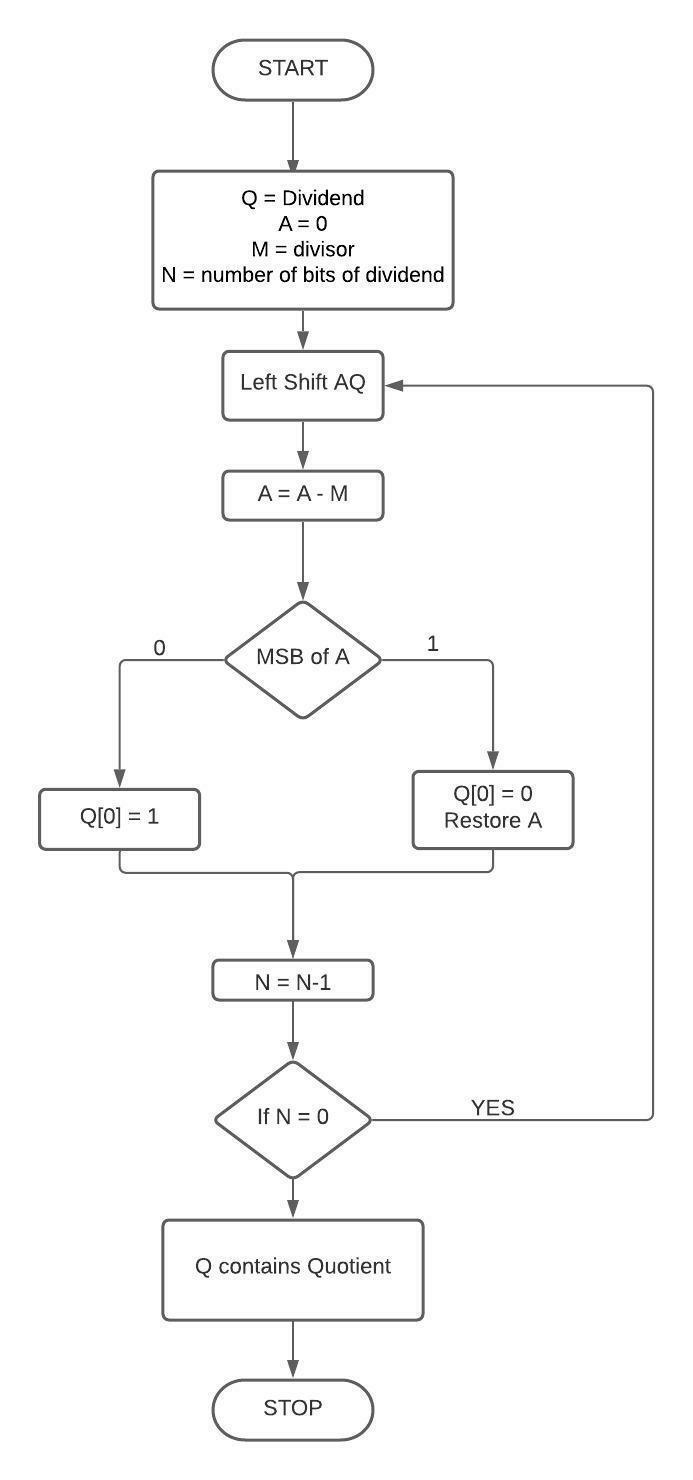
示例
上述方法的 C++ 代码
#include <iostream>
using namespace std;
int main(){
// initializing all the variables with Dividend = 9, Divisor = 2.
int Q = 8,q=1,M=3;
short N = 4;
int A = Q;
M <<= N;
// loop for division by bit operation.
for(int i=N-1; i>=0; i--) {
A = (A << 1)- M;
// checking MSB of A.
if(A < 0) {
q &= ~(1 << i); // set i-th bit to 0
A = A + M;
} else {
q |= 1 << i; // set i-th bit to 1
}
}
cout << "Quotient: "<< q;
return 0;
}输出
Quotient: 2
结论
在本教程中，我们讨论了无符号整数的恢复除法算法。我们讨论了一种使用流程图和应用位运算来解决此问题的简单方法。我们还讨论了此问题的 C++ 程序，我们可以使用 C、Java、Python 等编程语言来完成。希望本教程对您有所帮助。
更新于： 2021 年 11 月 26 日
1K+ 浏览量
广告