数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
服装研究
法律研究使用Python求解热力学第一定律
热力学第一定律与能量守恒有关，即如果某种形式的能量消失，则该能量将以其他形式出现。在热力学中，我们主要关注热量、功和内能。热量和功是能量的形式，也称为“能量传递”，因此它们是路径函数。系统不能储存它们，而内能是系统的属性，系统可以储存内能。
对于封闭系统，第一定律写成：
$$\mathrm{\Sigma Q=\Sigma W}$$
但这仅适用于经历循环的封闭系统。对于一个过程，可以写成：
$$\mathrm{Q_{1-2}=\triangle U+W_{1-2}}$$
在我们开始建模之前，应该知道如何为不同的过程建模功和热量。让我们首先做到这一点。
如果系统对外部环境的唯一影响可以简化为重量增加，则称系统进行了热力学功。在实际情况下，重量可能不会被提升，但效果仍然可能是提升重量。功可能是由系统完成的，也可能是作用于系统的，这取决于方向。前者被认为是正功，后者被认为是负功。
功是路径函数，因为它取决于两个状态之间的路径以及初始状态和最终状态。在本文中，我们将关注非耗散/位移功。它指的是封闭系统 p-v 图下的区域。
对于由过程 $pv^{n}$=常数表示的通用多方过程，所做的功取决于指数 𝑛。下表将根据指数 𝑛 说明不同的过程。
n |
过程 |
p−v 关系 |
|---|---|---|
0 |
等压过程 (p=常数) |
p = c |
1 |
理想气体的等温过程 (T=常数) |
pv =c |
1.4 |
绝热过程 (无热量交换) |
$\mathrm{pv^{y}\:=c}$ |
∞ |
等容过程 (体积恒定) |
v = c |
为了导出如公式 (3) 所示的功相互作用，典型的方法是从起始状态到最终状态积分过程。
$$\mathrm{W=\int ^{2}_{1}pdv}$$
因此，下表包含不同过程功相互作用的列表。
过程 |
p-v 关系 |
|---|---|
等压过程 (p = c) |
$\mathrm{p(v_{2}-v_{1})}$ |
理想气体的等温过程 (pv=c) |
$\mathrm{p_{1}v_{1}\mathbb{I}n\frac{v_{2}}{v_{1}}=p_{1}v_{1}\mathbb{I}n\frac{p_{1}}{p_{2}}}$ |
多方过程 ($pv^{n}=c)$ |
$\mathrm{\frac{\mathrm{p_{1}v_{1}-p_{2}v_{2}}}{n-1}}$ |
绝热过程 ($pv^{y}=c$) |
$\mathrm{\frac{\mathrm{p_{1}v_{1}-p_{2}v_{2}}}{\gamma -1}}$ |
等容过程 (v=c) |
0 |
热传递定义为由于温度差异而发生的系统与其周围环境之间的能量转移。传导、对流和辐射是其三个主要分类。
进入系统的热量被认为是正的，而离开系统的热量被认为是负的。当系统不与周围环境交换热量时，则称其经历绝热过程。将单位质量物质的温度提高一度所需的热量称为比热。
比热的表达式如公式 (4) 所示。物质的热容用符号 𝐶 (𝐶=𝑚𝑐) 表示，它是质量和比热的乘积。对于固体和液体，比热不受过程的影响；但是，对于气体，必须根据方法限定比热。因此，对于气体的恒压和恒容过程，它有所不同。
$$\mathrm{Q=mc\Delta t}$$
潜热 (L) 是每单位质量改变物质相所需的热量。潜热转换不会导致温度或压力的变化。
相变过程中单位质量物质的总热量相互作用由下式给出：
$$Q=mL$$
使用Python编程评估热量和功
下表显示了查找功和热量相互作用的不同Python函数。此外，它们还将用于绘制过程及其下方的面积。
from pylab import *
# Font and size
font = {'family' :'Times New Roman','size' : 16}
rc('font', **font)
# Constant Volume Process
def w_cv(p1,p2,v):
"""
Function for constant volume process
Input: Pressure limits p1 & p2 (in kPa) and volume (m^3)
Output: Work output and p-v plot
"""
figure(1,figsize=(7.20,4.80))
p=linspace(min(p1,p2),max(p1,p2),30)
v=zeros(30)+v
plot(v,p,'k-',linewidth=4)
xlabel('Volume (m$^3$)')
ylabel('Pressure (kPa)')
show()
return 0
# Constant Pressure Process
def w_cp(p,v1,v2):
"""
Function for constant pressure process
Input : Volume limits v1 & v2 (m^3) and pressure (kPa)
Output: Work output and p-v plot
"""
work = p*(v2-v1)
figure(2,figsize=(7.20,4.80))
v=linspace(min(v1,v2),max(v1,v2),30)
p=zeros(30)+p
plot(v,p,'k-',linewidth=4)
fill_between(v,p,color='red',alpha=0.3)
xlabel('Volume (m$^3$)')
ylabel('Pressure (kPa)')
show()
return round(work,3)
# Constant Temperature Process
def w_ct(p1,v1,v2):
"""
Function for constant temperature process
Input : Initial pressure (kPa) and volume (m^3) and final volume (m^3)
Output: Work output and p-v plot
"""
work = p1*v1*log(v2/v1)
figure(2,figsize=(7.20,4.80))
v=linspace(min(v1,v2),max(v1,v2),30)
c=p1*v1
p=c/v
plot(v,p,'k-',linewidth=4)
fill_between(v,p,color='red',alpha=0.3)
xlabel('Volume (m$^3$)')
ylabel('Pressure (kPa)')
show()
return round(work,3)
# Polytropic Process
def w_pol(p1,p2,v1,v2,n):
"""
Function for polytropic process
Input : p1 & p2 (kPa), v1 & v2 (m^3), and n (m^3)
If the process is adiabatic write n=1.4
Output: Work output and p-v plot
"""
work = (p1*v1-p2*v2)/(n-1)
figure(2,figsize=(7.20,4.80))
v=linspace(min(v1,v2),max(v1,v2),30)
c=p1*v1**n
p=c/v**n
plot(v,p,'k-',linewidth=4)
fill_between(v,p,color='red',alpha=0.3)
xlabel('Volume (m$^3$)')
ylabel('Pressure (kPa)')
show()
return round(work,3)
# Sensible Heat Transfer
def q_sh(m,c,T1,T2):
"""
Function for the evaluation of sensible heat transfer
Input : mass (m), sp. heat (c), initial temp (T1), final temp (T2)
Output: heat transfer
"""
return m*c*(T2-T1)
# Heat transfer during phase change
def q_mel_sol(m,Ti,Tf,T_pc,c_bpc,c_apc,L):
"""
Function for the evaluation of heat transfer during phase change
Input: mass (m), initial temp (Ti), final temp (Tf),
phase change temp (T_pc), sp. heat below phase change (c_bpc),
sp. heat above phase change (c_apc), latent heat (L)
Output: heat interaction
"""
if Ti>Tf:
print('Process is either freezing or condensation')
return m*(c_bpc*(T_pc-Ti)-L+c_apc*(Tf-T_pc))
else:
print('Process is either melting or vaporization')
return m*(c_bpc*(T_pc-Ti)+L+c_apc*(Tf-T_pc))
让我们看看如何通过两个例子来实现这些函数。
示例 1
1.5 kg 的空气根据等温过程从 0.2 MPa 压缩到 1 MPa。初始点的空气密度为 1.21 kg/m3。求所做的功，并在 p-v 图中绘制。
解决方案
程序如下：
# Input Data
m=1.50 # kg
p1=0.2E3 # kPa
p2=1.0E3 # kPa
ρ1=1.21 # kg/m^3
# Volume at the beginning
v1=m/ρ1
# Volume at end of process
v2=(p1*v1/p2)
# Given Process is isothermal
# The function will be: w_ct
Work = w_ct(p1,v1,v2)
print('Work output = ', Work)
执行后，您将得到以下**输出**：
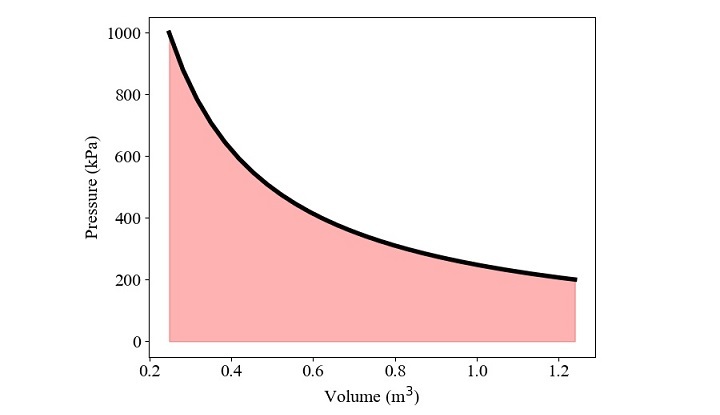
Work output = -399.034
示例 2
650 kg 的金枪鱼在 5°C 下冷冻并储存在 -12°C。冰点以上和以下 (-2°C) 的比热分别为 3.182 和 1.717 kJ/kg-K。对于 234.5 kJ/kg 的熔化潜热，需要评估从金枪鱼中去除的净热量。
解决方案
解决上述问题的 Python 程序如下：
# Input data
m=650 # kg
Ti=5 # deg C
Tf=-12 # deg C
T_pc=-2 # deg C
c_bpc=3.182 # kJ/kg
c_apc=1.717 # kJ/kg
L=234.5
# Function calling
Q_net=q_mel_sol(m,Ti,Tf,T_pc,c_bpc,c_apc,L)
print("Q = ",Q_net)
输出
程序**输出**将是：
Process is either freezing or condensation Q = -178063.6
现在的问题是如何在代码中建模公式 1 和 2。由于您已经评估了热量和功的函数，因此您可以很容易地建模第一定律。让我们通过两个例子来解决它。
示例 3
在示例 1 中，系统损失了 5 kJ 的热量，然后评估系统的内能变化。
解决方案
首先，功的代码保持不变（如示例 1 中一样），唯一变化的是公式 1 的实现，因此完整代码将是：
# Input Data
m=1.50 # kg
p1=0.2E3 # kPa
p2=1.0E3 # kPa
ρ1=1.21 # kg/m^3
# Volume calculation at point 1
v1=m/ρ1
# Calculation of volume at point 2
v2=(p1*v1/p2)
# Evaluation of W_12
# The function used is w_ct
w = w_ct(p1,v1,v2)
# Q_12
Q=-5
# Equation 1 says:
Δu=Q-w
print(f"Δu = {Δu} kJ")
输出
程序输出将是：
Δu = 394.034 kJ
因此，系统的内能增加了 394.034 kJ。
示例 4
一个封闭系统经历三个热交换和两个功交换，如下所示：
Q (kJ) |
+10 |
-30 |
-40 |
W (kJ) |
+100 |
-50 |
? |
找到缺失的能量相互作用。
解决方案
from numpy import *
nq=int(input("Enter number of heat interactions known: "))
nw=int(input("Enter number of work interactions known: "))
Q=empty(nq)
W=empty(nw)
for i in range(nq):
Q[i]=float(input(f' Enter {i+1} heat interaction: '))
ΣQ=sum(Q)
for i in range(nw):
W[i]=float(input(f' Enter {i+1} work interaction: '))
ΣW=sum(W)
# Missing Work interaction
W=ΣQ-ΣW
print(f' Missing work interaction : {W} kJ')
输出
程序输出将是：
Enter number of heat interactions known: 3 Enter number of work interactions known: 2 Enter 1 heat interaction: 10 Enter 2 heat interaction: -30 Enter 3 heat interaction: -40 Enter 1 work interaction: 100 Enter 2 work interaction: -50 Missing work interaction: -110.0 kJ
结论
在本教程中，我们解释了如何建模和绘制功相互作用和热量相互作用。此外，我们还通过两个问题了解了如何对开放系统的第一定律的公式 1 和 2 进行实现。
1000+ 次浏览
