数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会研究
服装研究
法律研究C++中的松鼠模拟
有一棵树、一只松鼠和几颗坚果。位置用二维网格中的单元格表示。你的目标是找到松鼠收集所有坚果并将它们一个接一个地放在树下的最小距离。松鼠一次最多只能拿一颗坚果，并且可以沿四个方向移动——上、下、左、右，到相邻的单元格。距离用移动次数表示。
因此，如果输入类似于高度：5 宽度：7 树的位置：[2,2] 松鼠：[4,4] 坚果：[[3,0], [2,5]]，则输出将为 12。
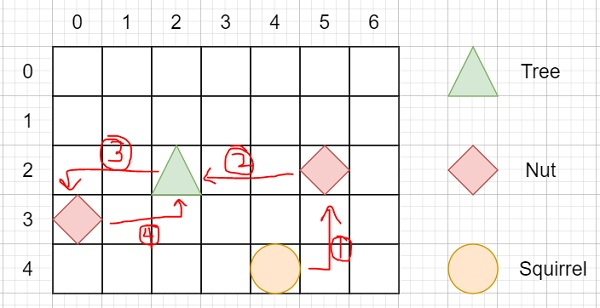
为了解决这个问题，我们将遵循以下步骤：
定义一个函数 calc()，它将接收 x1、y1、x2、y2。
返回 |x1 - x2| + |y1 - y2|
定义一个函数 minDistance()，它将接收高度、宽度、一个树数组、一个松鼠数组和一个二维坚果数组。
ret := 0
maxDiff := -inf
初始化 i := 0，当 i < 坚果数量时，更新（i 增加 1），执行：
dist := calc(tree[0], tree[1], nuts[i, 0], nuts[i, 1])
ret := ret + 2 * dist
maxDiff := maxDiff 与 2 * dist - (dist + calc(nuts[i, 0], nuts[i, 1], sq[0], sq[1])) 之间的最大值
返回 ret - maxDiff
示例
让我们看看下面的实现，以便更好地理解：
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int calc(int x1, int y1, int x2, int y2){
return abs(x1 - x2) + abs(y1 - y2);
}
int minDistance(int height, int width, vector<int>& tree, vector<int>& sq, vector<vector>& nuts) {
int ret = 0;
int maxDiff = INT_MIN;
for (int i = 0; i < nuts.size(); i++) {
int dist = calc(tree[0], tree[1], nuts[i][0],
nuts[i][1]);
ret += 2 * dist;
maxDiff = max(maxDiff, 2 * dist - (dist + calc(nuts[i][0], nuts[i][1], sq[0], sq[1])));
}
return ret - maxDiff;
}
};
main(){
Solution ob;
vector<int> v = {2,2}, v1 = {4,4};
vector<vector<int>> v2 = {{3,0}, {2,5}};
cout << (ob.minDistance(5,7,v, v1, v2));
}输入
5, 7, {2,2},{4,4}, {{3,0}, {2,5}}输出
12
更新于：2020年11月16日
263 次查看
广告