Swift程序计算平行四边形的面积

本教程将讨论如何编写一个Swift程序来计算平行四边形的面积。平行四边形是由平行线构成的四边形。

其中对边平行且相等，平行四边形的对角相等。它有三种类型 - 矩形、正方形和菱形。

在平行四边形中，面积是指在二维平面上平行四边形边界或边内部所包围的空间。假设我们有一个茶托，现在平行四边形的面积可以帮助我们找到覆盖茶托顶部需要多少油漆。我们可以使用以下方法计算平行四边形的面积：

使用高度

使用边的长度

使用对角线

使用高度计算平行四边形的面积

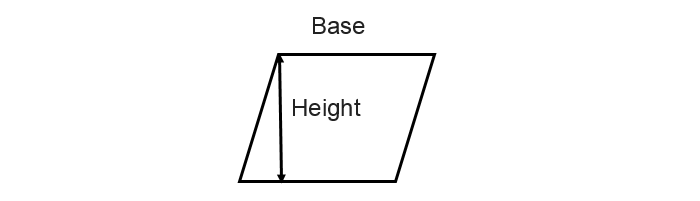
我们可以借助高度计算平行四边形的面积。假设我们有两组平行边P和Q，它们之间的距离为H。H也被称为平行四边形的高度。因此，平行四边形的面积是底和高的乘积。

公式

以下是平行四边形面积的公式

Area = Base x Height
Or
Area = Q x H

其中Q是底，H是平行四边形的高度。

使用高度计算平行四边形面积的算法

  • 步骤1 - 定义两个变量表示底和高

  • 步骤2 - 为这些变量赋值

  • 步骤3 - 使用高度实现平行四边形面积公式（面积 = 底 x 高）

  • 步骤4 - 打印输出

示例

以下程序演示了如何借助高度计算平行四边形的面积。

import Foundation
import Glibc

var base = 12
var height = 10

var AreaOfParallelogram = base * height

print("Base of the parallelogram:", base)
print("Height of the parallelogram:", height)
print("Final area of the parallelogram: ", AreaOfParallelogram)

输出

Base of the parallelogram: 12
Height of the parallelogram: 10
Final area of the parallelogram: 120

在上面的代码中，我们使用如下代码所示的数学公式计算平行四边形的面积：

var AreaOfParallelogram = base * height

这里，平行四边形的底是12，平行四边形的高度是10。因此，平行四边形的面积是120。

使用边长计算平行四边形的面积

我们可以借助其相邻边及其之间的夹角计算平行四边形的面积。假设我们有两条相邻边P和Q，以及它们之间的夹角为O（ᶿ）（以弧度表示）。因此，平行四边形的面积是这两条边和夹角的乘积。

公式

以下是平行四边形面积的公式

Area = Side1 x Side2 x sin(ᶿ)
Or
Area = P x Q x sin(ᶿ)

其中P和Q是边的长度，O是它们之间的夹角。

使用边长计算平行四边形面积的算法

  • 步骤1 - 定义三个变量（边1、边2和角度）

  • 步骤2 - 为这些变量赋值

  • 步骤3 - 使用边长实现平行四边形面积公式（面积 = 边1 x 边2 x sin(ᶿ)）

  • 步骤4 - 打印输出

示例

以下程序演示了如何借助边长计算平行四边形的面积。

import Foundation
import Glibc

var side1 = 12.0
var side2 = 10.0
var angle = 45.0

var AreaOfParallelogram = side1 * side2 * sin(angle * (Double.pi / 180.0))

print("Side 1 of the parallelogram:", side1)
print("Side 2 of the parallelogram:", side2)
print("Angle of the parallelogram:", angle)
print("Final area of the parallelogram: ", AreaOfParallelogram)

输出

Side 1 of the parallelogram: 12.0
Side 2 of the parallelogram: 10.0
Angle of the parallelogram: 45.0
Final area of the parallelogram: 84.85281374238569

在上面的代码中，我们使用如下代码所示的数学公式计算平行四边形的面积：

var AreaOfParallelogram = side1 * side2 * sin(angle * (Double.pi / 180.0))

这里，平行四边形的两条边长分别为12和10，夹角为45度。因此，平行四边形的面积为84.85281374238569。在代码中，我们使用以下公式将度数转换为弧度。

Radian = degrees *(Double.pi / 180.0)

使用对角线计算平行四边形的面积

我们可以借助对角线计算平行四边形的面积。平行四边形有两条对角线，它们彼此相交成一定角度。假设我们有两条对角线D1和D2，以及它们之间的夹角为O（以弧度表示）。因此，平行四边形的面积是这两条对角线的长度及其夹角的乘积。

公式

以下是平行四边形面积的公式：

Area = (Diagonal1 x Diagonal2 x sin(ᶿ))/2
Or
Area = (D1 x D2 x sin(O))/2

其中D1和D2是边的长度，O是它们之间的夹角。

使用对角线计算平行四边形面积的算法

  • 步骤1 - 定义三个变量（对角线1、对角线2和角度）

  • 步骤2 - 为这些变量赋值

  • 步骤3 - 使用对角线实现平行四边形面积公式（面积 = (对角线1 x 对角线2 x sin(ᶿ))/2）

  • 步骤4 - 打印输出

示例

以下程序演示了如何借助对角线计算平行四边形的面积。

import Foundation
import Glibc

var diagonal1 = 35.0
var diagonal2 = 40.0
var angle = 30.0
var AreaOfParallelogram = 1/2 * diagonal1 * diagonal2 * sin(angle * (Double.pi / 180.0))

print("Diagonal 1 of the parallelogram:", diagonal1)
print("Diagonal 2 of the parallelogram:", diagonal2)
print("Angle:", angle)
print("Final area of the parallelogram: ", AreaOfParallelogram)

输出

Diagonal 1 of the parallelogram: 35.0
Diagonal 2 of the parallelogram: 40.0
Angle: 30.0
Final area of the parallelogram: 349.99999999999994

在上面的代码中，我们使用如下代码所示的数学公式计算平行四边形的面积：

var AreaOfParallelogram = 1/2 * diagonal1 * diagonal2 * sin(angle * (Double.pi / 180.0))

这里，平行四边形的两条对角线长分别为35和40，夹角为30度。因此，平行四边形的面积为349.99999999999994。在代码中，我们使用以下公式将度数转换为弧度。

Radian = degrees *(Double.pi / 180.0)

更新于： 2022年8月2日

580 次浏览

开启你的职业生涯

通过完成课程获得认证

立即开始
广告