使用平行四边形定则求解给定物体的重量

---

引言

平行四边形定则向量法有助于确定物体的方向，并有助于建立物体重量的概念。根据向量加法的平行四边形定则，如果两个向量可以用平行四边形的相邻边来表示其大小和方向，那么其合力的大小和方向可以用平行四边形的对角线来表示。本教程将帮助您理解如果向量沿相同方向绘制，结果将显示为平行四边形的对角线。本教程的主要目的之一是通过力的定律来确定给定物体的重量。

平行四边形定则向量

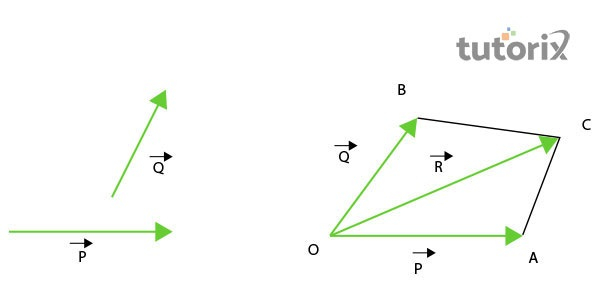
图1：平行四边形定则向量

平行四边形是用于测量本教程中给出的不同材料的有用原理之一。平行四边形定则指出，平行四边形四边长度的平方和等于两条对角线长度的平方和。在欧几里得几何中，平行四边形必须具有相等的对边（Oller，2019）。例如，在本教程中，如果取ABCD为平行四边形，则AB = DC且BC = AD。因此，平行四边形的定义如下：$\mathrm{2(AB)^{2} + 2 (BC)^{2} = (AC)^{2} + (BD)^{2}}$。

所用材料

为了根据平行四边形定则测量任何给定物体的重量，可以使用不同的材料。以下材料具有不同的用途，并有助于合成向量。想要进行计算的学生需要适当准备铅垂线、待测重的物体、两个带刻度的砝码盘。下一步，学生需要准备白纸、刻度尺、结实的细线和图钉进行绘图（Parween等人，2018）。此外，还需要反光镜条和铅笔来完成测量。

理论

$\mathrm{S\: = \:\sqrt{(P^{2}\: +\: Q^{2} \: +\: 2PQcos\theta)}}$

S为未知重量；P和Q为平衡砝码重量

步骤

为了通过使用平行四边形定则向量的实验确定给定物体的重量，需要遵循以下步骤。需要将Gravesand装置垂直放置在桌面上。必须确保滑轮处于良好工作状态。需要用图钉将一张白纸固定在滑轮之间（Zhang等人，2021）。将砝码盘的钩子系在细线的两端。需要通过将另一根细线系在穿过滑轮的细线的中间来悬挂未知重量。

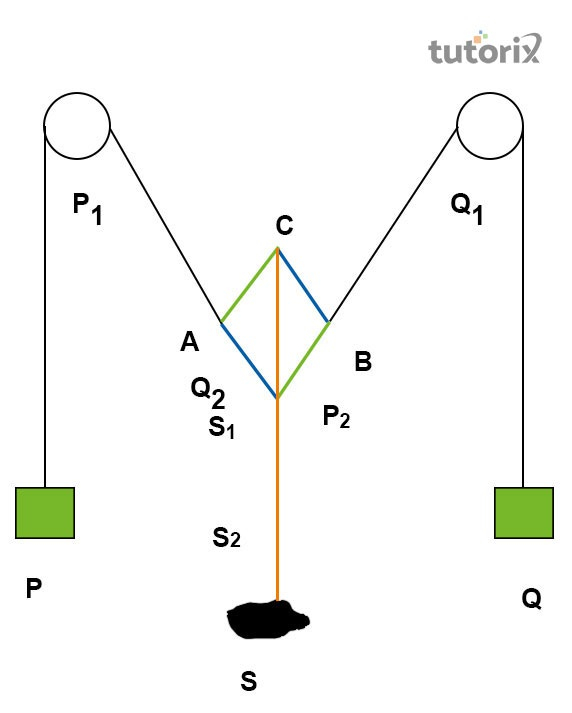
图2：实验图

将带刻度的砝码挂在砝码盘上，并调整砝码的重量，直到结点到达纸张的中心。在每根细线下方放置一块平面镜，以确定力的方向。将眼睛放在细线覆盖的地方，标记反光镜条的末端。然后，将每对点连接起来，它们可以在O点相遇。然后标记OA和OB的边。通过对角线连接标记点来测量OC，并使用弹簧秤来额外确保物体的重量。为了观察实验的重复性，需要多次更改连接在P点和Q点的砝码重量。

观察和计算

序号	力		边长			合力R	未知重量S	弹簧秤测得的重量	误差
	P	Q	OA	OB	OC
1.	145	145	3.5	3.5	3.6	180	200	205	5

表1：观察表

弹簧秤的最小刻度和零点误差将以克为单位确定（Cohen等人，2021）。所用刻度为1厘米，相当于50克。根据上述观察表，发现OC = 3.6厘米，R = 50 × 3.6 = 180克。未知重量被认为等于200克，而平均未知重量计算为$\mathrm{S\:=\:\frac{S_{1}+S_{2}+S_{3}}{S} \:= \:200g}$。弹簧秤测得的重量与205克相似，差值为5克。

结论

本教程阐明了向量的一些因素，这些因素具有解决重量测量的潜在方程。大多数情况下，给定的材料是方程的有效部分，其中功能组件依赖于Gravesand装置。基于力的平行四边形定则，上述材料是有用的，需要包含具有功能组件的测量值，并且重量测量的建立遵循上面也提供的步骤。此外，还讨论了如何通过应用向量平行四边形定则以及观察结果来观察材料的重量。

常见问题

Q1. 在此实验过程中需要注意哪些事项？

A1. 实验板的位置需要稳定且垂直，滑轮必须具有较低的摩擦系数。纸张的中间需要有结点O，并且需要使用箭头来表示方向。

Q2. 什么是标量？

A2. 在物理学术语中，标量被定义为只有大小而没有方向的物理量。