光线穿过玻璃平板的路径追踪

---

引言

光线路径变化的性质是基于这样一个实验来评估的：该实验追踪了光线穿过玻璃平板时的路径。根据斯涅尔折射定律，光的性质随其传播介质而变化。解读结果有助于人们理解折射值变化背后的原因。

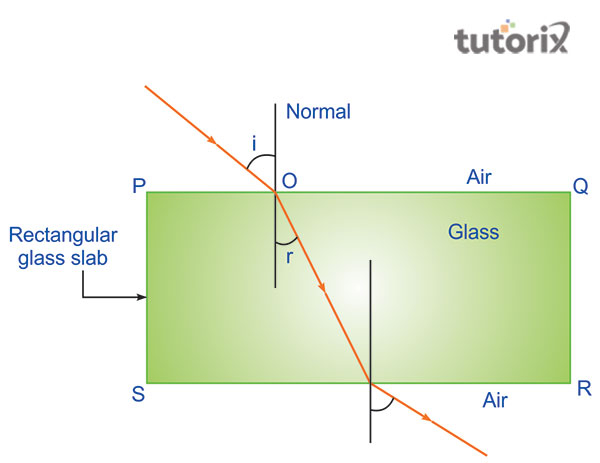
图1：光线穿过玻璃平板

目的

本实验的目的是追踪光线穿过矩形玻璃平板时的精确路径。本实验的另一个目的是测量入射角、出射角和折射角的精确值，并最终解释结果。

理论

该理论基于与折射相关的斯涅尔定律。该定律的两个最重要的方面有助于描述折射的基本概念。折射的第一定律指出，法线、入射光线和折射光线位于同一直线上 (Rehm, 2020)。根据斯涅尔定律，入射角正弦之比与折射角正弦之比为常数。这一事实也可以表示为 sin i / sin r = 常数。

侧向位移

当光线从折射介质出射时，其路径上的垂直位移与侧向位移有关。

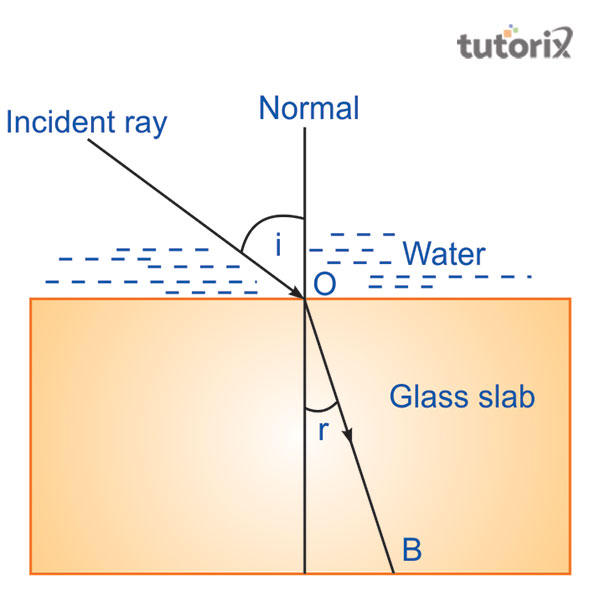
图2：入射光线穿过玻璃平板

光的折射

当光线从一种介质传播到另一种介质时，它常常会改变其路径。介质的密度在产生光的折射中起着重要作用 (Ahmadi et al. 2020)。当光线从光密介质移动到光疏介质时，就会发生折射。

所需材料

• 5-6枚大头针
• 一块绘图板
• 刻度尺
• 图钉
• 白纸
• 一块矩形玻璃平板
• 铅笔
• 量角器

实验过程

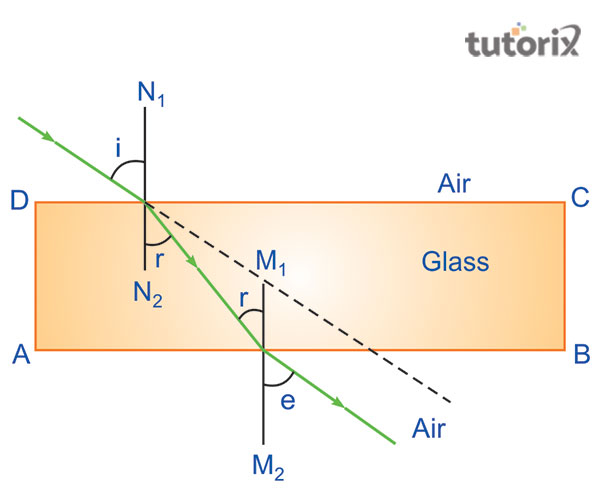
图3：光线路径的折射

在本实验中，折射发生在空气-玻璃界面和玻璃-空气界面。如图所示，光线以斜角入射到DC面上，并向其法线方向弯曲 (Zhdanov et al. 2018)。在玻璃平板内部，入射光线平行折射。折射发生后，光线偏离其法线方向。这两种折射都遵循折射定律。

示意图

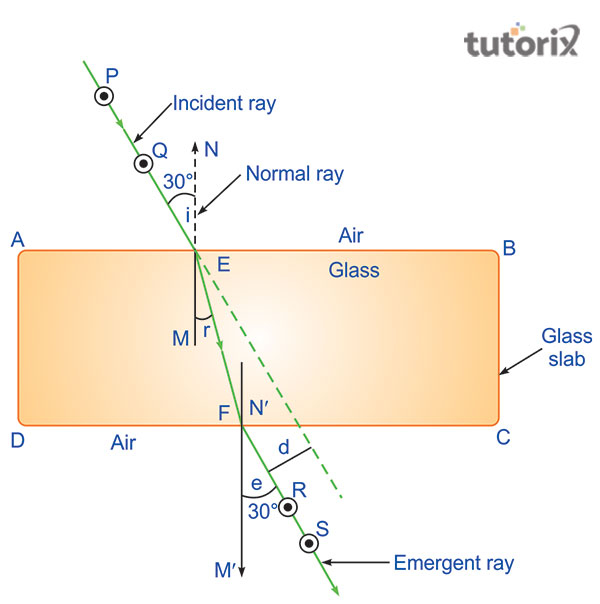
图4：追踪光线的路径

首先，取一张白纸，用图钉将其固定在绘图板上。用铅笔画出玻璃平板的轮廓。在本实验中，矩形玻璃平板的四个轮廓点为ABCD。在AB边上标出E点，并画出垂直于法线的EN线。用量角器画一个30⁰的角。在P点和Q点固定大头针，距离法线约4-5厘米。这两个点位于通过30⁰角得到的射线上。

然后，将玻璃平板放置在ABCD处，透过其CD面观察以固定R点和S点。应以所有大头针位于同一直线的方式设置这些大头针。在PQR和S周围画一个小圆圈，然后取下所有大头针。此时应移除玻璃平板。

将R点和S点正确连接，使这些线在CD上的F点处相交。在F点处画出垂直于NM的线。将包括E和F在内的所有点用铅笔连接。AB和CD周围形成了两个不同的角度。测量折射角、出射角和入射角。在此过程中，还会发现发生了侧向位移，可以通过将PQ射线平行于FRS延长来获得。同样的过程也重复进行45度和60度的测量。

观察表

入射角	出射角	折射角
600	59.80	560	0.20
450	44.80	430	0.20
300	300	280	00

表1：实验观察表

总结

为了正确地进行该实验并确保实验的顺利进行，需要遵循一些注意事项，其中确保矩形玻璃平板的平整度非常重要。也要保持玻璃平板的清洁，以便于放置大头针。入射角应保持在30度到60度之间。所有大头针的底部应位于同一直线上。也要确定侧向位移的值。

常见问题

Q1. 出射角和入射角之间有什么关系？

这两个角的值是相等的。其中一个角的值等于另一个角的值。小的误差会导致这两个角的值出现差异。

Q2. 彩虹形成的原因是什么？

在彩虹的形成过程中，折射起着重要的作用。微小的水滴导致光的这种折射，最终导致彩虹的形成。

Q3. 光的折射中没有偏斜的条件是什么？

在某个时刻，光线垂直于折射面。此时，光线不会发生偏转。

Q4. 追踪光线路径实验中需要避免哪些常见的错误？

确保玻璃平板中没有气泡。也要确保用量角器测量的准确性。