(a) 绘制带标签的光线图，展示一束光斜射到玻璃板一个表面上的路径。(b) 计算玻璃板材料的折射率。已知光线穿过玻璃板的速度为 2 x 10⁸ m/s，在空气中的速度为 3 x 10⁸ m/s。(c) 如果透镜的焦度为 -2.5 D，计算其焦距。

(a) 以下是展示光线斜射到玻璃板一个表面上路径的带标签光线图

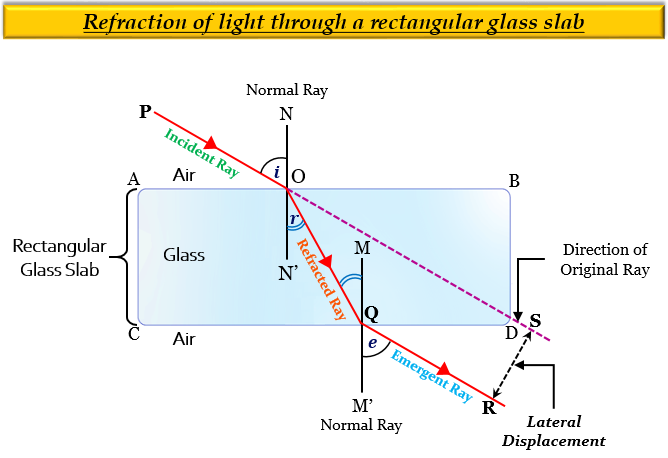
(b) 已知

光线穿过玻璃板的速度 = $2\times {10^8m/s}$

光线在空气中的速度 = $3\times {10^8m/s}$

求解：玻璃板材料的折射率，$n_{ga}$。

解答

我们知道折射率 $(n)$ 的公式如下：

介质的折射率 = 真空/空气中光速 / 介质中光速

这里，

$n_{ga}=\frac {空气中光速}{玻璃中光速}$

将给定值代入表达式中，我们得到：

$n_{ga}=\frac {3\times {10^8m/s}}{2\times {10^8m/s}}$

$n_{ga}=\frac {3}{2}$

$n_{ga}=1.5$

因此，玻璃板材料的折射率 $n_{ga}$ 为 1.5。

(c) 已知

透镜的焦度，$P$ = $-$2.5 D

求解：焦距，$f$。

解答

我们知道透镜焦度的公式如下：

$P=\frac {1}{f}$

将 $f$ 的值代入公式，我们得到：

$-2.5=\frac {1}{f}$

$f=-\frac {1}{2.5}$

$f=-\frac {10}{25}$

$f=-0.4m$

因此，透镜的焦距 $f$ 为 -0.4m。

Tutorialspoint

更新于：2022年10月10日

467 次浏览

开启你的职业生涯

完成课程获得认证

开始学习