数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究CRC 的计算算法是什么？
循环冗余校验 (CRC)
循环冗余校验 (CRC) 是一种由 W. Wesley Peterson 于 1961 年发明的分组码。它通常用于检测通过电信网络和存储设备传输的数据中意外发生的更改。
CRC 涉及将要发送的数据位与通信系统商定的预定除数进行二进制除法。除数是使用多项式生成的。因此，CRC 也称为多项式码校验和。
在通过网络通道发送消息之前，发送方使用 CRC 对消息进行编码。接收方解码传入的消息以检测错误。如果消息无错误，则接受该消息；否则，接收方要求重新传输该消息。
该过程说明如下
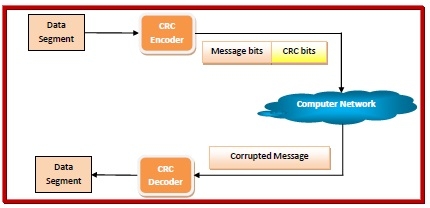
CRC 计算
当使用 CRC（多项式码）对消息进行编码时，会使用一个称为生成多项式 𝐺G(x) 的固定多项式。的值由发送方和接收方共同商定。一个 k 位字由一个多项式表示，该多项式的范围从 X0 到 xk-1。此多项式的阶数是最高系数的幂，即 (K-1) G(x) 的长度应小于其编码的消息的长度。此外，其 MSB（最高有效位）和 LSB（最低有效位）都应为 1。在编码过程中，CRC 位附加到消息中，以便生成的帧可被 G(x) 整除。
使用 CRC 进行编码的算法
通信双方商定消息的大小，M(x) 和生成多项式， G(x)。
如果 r 是 G(x) 的阶数，则 r 位附加到 M(x) 的低阶端。这使得块大小为位，其值为 xrM(x)。
块 xrM(x) 使用模 2 除法除以 G(x)。
除法后的余数使用模 2 加法添加到 xrM(x) 中。结果是要传输的帧， T(x)。编码过程使完全可被 G(x) 整除。
使用 CRC 进行解码的算法
接收方使用模 2 除法将传入的数据帧 T(x) 单元除以 G(x)。在数学上，如果 E(x) 是错误，则执行 [M(x) + E(x)] 除以 G(x) 的模 2 除法。
如果没有余数，则表示 E(x)。接受数据帧。
余数表示 E(x) 的非零值，换句话说，表示存在错误。因此，数据帧被拒绝。然后，接收方可能会向发送方发送错误确认以进行重传。
6K+ 次查看
