迪杰斯特拉算法是什么？

最短路径路由算法是一种广泛使用的非自适应路由算法，它根据迪杰斯特拉重要的最短路径算法来路由数据包。在这种方法中，到达节点的数据包会选择网络中到特定目的地的最短路径之一。

这种方法的缺点是它没有充分考虑网络流量的变化。例如，排队会在中间节点造成拥塞，导致数据包在到达目的地之前被延迟。在这种情况下，最好让数据包选择可能不是最短路径但最终可以更快传输时间的路径。

最短路径路由 (SPR) 算法根据网络中各种矩阵表示的成本度量来评估路由。

设 V 为有向图的所有边的集合，C[S, V] 为到任何待评估节点的最少成本（最短路径）矩阵。最初，在添加其路由之前，每条边（节点）将到任何其他边的最短路径成本设置为无穷大，即 ∞。假设有向图中有 n 条边，每条边都通过选择其邻居 x（属于 V – S）来评估到不同节点的最短路径成本，该邻居 x 从 S 到 x 的权重 W 值最低。它使用以下公式评估每条边 (S, x)（S 的邻居）的路由。

D [V] = min (D [V], D [V] + C(S, V))

C (S, V) 是连接到 S 的顶点的成本。此过程一直持续到访问所有有向图边为止。当算法中断时，网络中的所有节点都必须找到每个节点的最短路径。

算法步骤

  • 源节点被初始化并用黑色圆圈表示。

  • 确定相邻节点的成本，并将其重新标记为源节点。

  • 通过检查相邻节点来确定最小标签，使其永久化并将其作为源节点。

例如，我们想从 A 获取 G。步骤如下：

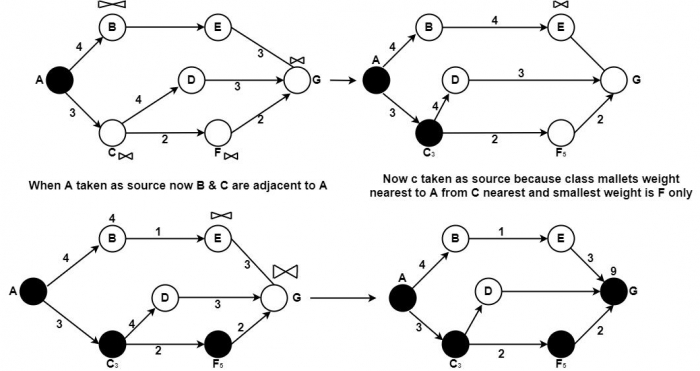
首先将 A 作为第一个源节点并将其加黑。然后是 C，然后是 F，G 离 F 最近，到达目的地的总权重为 7（从 A 到 G），最短路径是 (A, C, F, G)，而不是 ABEG。

更新于：2021年5月5日

浏览量：572

开启您的职业生涯

完成课程获得认证

开始学习
广告