数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究在编译器设计中，DFA 的最小化是什么？
最小化意味着减少 DFA 中的状态数。我们必须检测 DFA 中那些存在或不存在都不会影响 DFA 接受的语言的状态。这些状态可以从 DFA 中消除。
算法：DFA 的最小化
输入 - DFA D1，具有一组状态 Q 和一组终结状态 F。
输出 - DFA D2，它接受与 D1 相同的语言，并尽可能具有最少的状态数。
方法
对状态集进行划分 'π'，分成两个子集 -
- 终结状态 'F'
- 非终结状态 'Q-F'
∴ π={F,Q−F}
应用以下过程从 π 生成 πnew。
对于 π 中的每个集合 S
划分 S 为子集，使得 S 中的两个状态 p 和 q 在 S 的同一个子集中，如果对于每个输入符号 'a'，状态 p 和 q 转移到 π 的同一个集合中的状态。它可以用形成的子集集替换 πnew 中的 S。
如果 πnew=π，则令 πfinal=π 并继续执行步骤 4。否则对 π =πnew 重复步骤 2。
从 πfinal 的每个集合中选择一个状态作为该集合的代表。
这些状态将是最小化 DFA D2 的状态。
示例 1 - 将以下 DFA 转换为最小化 DFA。
解决方案
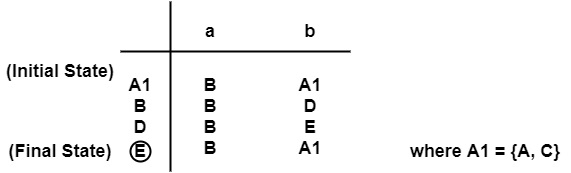
制作状态转换表
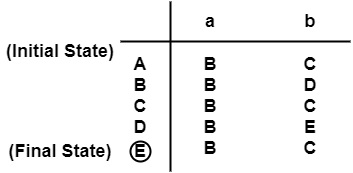
对状态集进行划分 'π'，即 π ={F,Q−F}
∴ π0={{E},{A,B,C,D}}
对于输入符号 a，在 π0 的 {A, B, C, D} 上
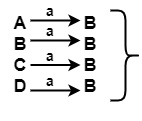
所有 B 都位于 π0 的同一集合 {A, B, C, D} 中
对于输入符号 b，在 π0 的 {A, B, C, D} 上
∴ π0 的 {A,B,C,D} 将被拆分为 {A,B,C} 和 {D}
π1={{E},{A,B,C},{D}}
对于输入 a，在 π1 的 {A, B, C} 上
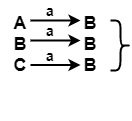
所有 B 都位于 π1 的同一集合中
对于输入 b 在 π1 的 {A, B, C} 上
∴ π1 中的 {A,B,C} 将被拆分为 {A, C} 和 {B}
∴ π2={{E},{A,C},{B},{D}}
检查 {A, C} 是否可以进一步拆分 (a)
- 对于输入 a，在 π2 的 {A, C} 上
对于输入 b，在 π2 的 {A, C} 上
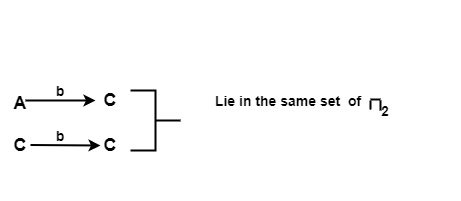
∴ {A,C} 不会被拆分
∴ π3={{E},{A,C},{B},{D}}
∴ π3=π2=πfinal={{E},{A,C},{B},{D}}
∴ 最小化 DFA 将有 4 个状态，对应于给定 DFA 的 5 个状态。
{A, C} 可以重命名为 A1
B D E
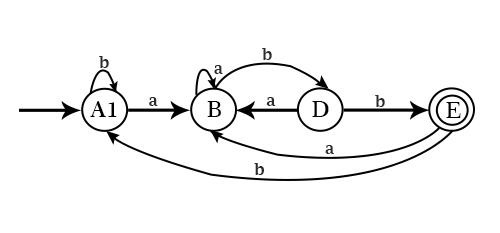
最小化 DFA 的状态，即 A1、B、D、E 将通过查看给定 DFA 表中的转换连接起来。
最小化或简化自动机将是
3K+ 次查看
