编译器设计中DFA的表示是什么？

确定性意味着对于每个输入，自动机都只有一个状态可以从其当前状态转换。在确定性有限自动机中，磁头只能向一个方向移动以扫描输入带上的符号。但在双向有限自动机的情况下，在扫描输入符号时，磁头的移动方向可以向右或向左，从其当前位置移动。

确定性有限自动机是一组 5 元组，定义如下：

M = (Q, Σ, δ, q₀, F)

• Q：有限控制中存在的一组非空有限状态 (q₀, q₁, q₂)。
• Σ：一组非空有限的输入符号。
• δ：这是一个转移函数，它接受两个参数，一个状态和一个输入符号，它返回一个由 ∴ δ: Q x Σ → Q 表示的单个状态。令 q 为传递给转移函数的状态，a 为输入符号。δ(q, a) = q。q 是函数的输出，它可能是相同的状态或新状态。
• $q_{0} \, \epsilon \, Q$ 是初始状态。
• $F \subseteq Q$ 是最终状态的集合。

有两种方法可以表示确定性有限自动机：

• 状态转换图

它是一个有向图或流程图，具有状态和边。状态转换图由 John Myhill 于 1957 年创建。状态转换图中的强路径是一系列形成路径的边，从某个起始状态开始，到某个最终状态结束。它可以集中字母串，以便标记路径中的每条边。它可以生成被此机器接受的单词。因此，它可以将状态转换图描述为以下内容的集合：

• 一组有限的状态，其中一个被命名为起始状态，其中一些被命名为最终状态。起始状态用带箭头的圆圈表示，最终状态用两个同心圆表示。示意图如下所示：

示例

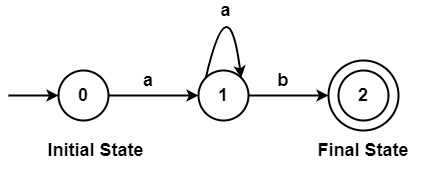
0、1、2→状态

0→初始状态

2→最终状态

a、b→输入符号

• 一个字母表 Σ，从中形成输入字符串的可能的输入字母。

• 一组有限的转换（标记边），它显示了如何根据读取定义的输入字母子字符串从一个状态转换到另一个状态。

• 状态转换表

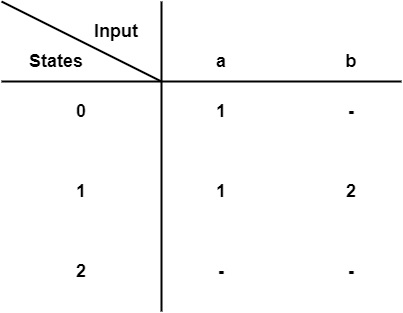
有限自动机可以用 5 元组 (Q, Σ, δ, q₀, F) 表示

• Q 是一组有限的非空状态。
• Σ 是一组有限的输入符号。
• $\delta$ 是转移函数。
• q₀ ∈ Q 是初始状态。
• F ⊆ Q 是最终状态的集合。

示例 - 设计接受字符串“abb”的有限自动机。

解决方案

状态 - Q = {q₀, q₁, q₂, q₃}

输入符号 - Σ = {a, b}

转移函数 $\delta$ - {$\delta$(q₀, a) = q₁,$\delta$ (q₁, b) = q₂, $\delta$(q₂, b) = q₃}

初始状态 - q₀

最终状态 (F) - {q₃}

Ginni

更新于：2021年10月29日

2K+ 浏览量

开启您的 职业生涯

通过完成课程获得认证

开始学习