数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时尚研究
法律研究什么是Scott-T变压器连接？
Scott-T连接是一种连接两个单相变压器以执行三相到两相转换和反之亦然的方法。在Scott连接中，两个单相变压器在电气上（而非磁性上）连接，其中一个变压器称为主变压器，另一个称为辅助或预激变压器。
Scott连接的连接图如图所示。主变压器是中心抽头变压器，位于D点，并连接到三相侧的Y和B线。因此，主变压器的一次绕组为YB，二次绕组为a1a2。预激变压器连接在线端子R和中心抽头点D之间。因此，预激变压器具有一次绕组RD和二次绕组b1b2。
Scott-T连接的相量图
Scott连接的相量图如图所示。
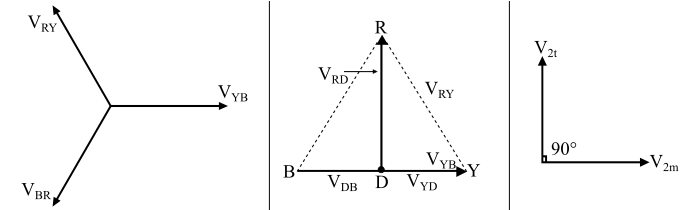
这里，三相平衡供电系统的线电压为：
$$\mathrm{𝑉_{𝑅𝑌} = 𝑉_{𝑌𝐵} = 𝑉_{𝐵𝑅} = 𝑉_{𝐿}}$$
设VYB为参考相量，则
$$\mathrm{𝑉_{𝑌𝐵} = 𝑉_{𝐿}\angle 0°}$$
$$\mathrm{𝑉_{𝑅𝑌} = 𝑉_{𝐿}\angle + 120°}$$
$$\mathrm{𝑉_{𝐵𝑅} = 𝑉_{𝐿}\angle − 120°}$$
该图还显示了主变压器和预激变压器一次绕组上的电压。由于中心抽头点D将主变压器一次绕组YB分成两半。因此，
$$\mathrm{YD段匝数 = DB段匝数 =\frac{𝑁_{𝑃}}{2}}$$
因此，电压VYD和VDB相等，并且与电压VYB同相，即
$$\mathrm{𝑉_{𝑌𝐷} = 𝑉_{𝐷𝐵} =\frac{𝑉𝐵𝐶}{2}=\frac{𝑉_{𝐿}}{2}\angle 0° \:\:… (1)}$$
现在，端子R和D之间的电压为
$$\mathrm{𝑉_{𝑅𝐷} = 𝑉_{𝑅𝑌} + 𝑉_{𝑌𝐷} = 𝑉_{𝐿}\angle 120° +\frac{𝑉_{𝐿}}{2}\angle 0°}$$
$$\mathrm{\Rightarrow\:𝑉_{𝑅𝐷} =[𝑉_{𝐿}(-\frac{1}{2}+𝑗\frac{√3}{2})]\:+\:[\frac{𝑉_{𝐿}}{2}(1\:+\:𝑗0)]}$$
$$\mathrm{\Rightarrow\: 𝑉_{𝑅𝐷} =𝑗\frac{√3}{2}𝑉_{𝐿}= 0.866\:𝑉_{𝐿}\angle 90° … (2)}$$
因此，预激变压器的一次电压VRD为主变压器电压的0.866倍，并且在时间上相差90°。
电压VRD施加到预激变压器的一次绕组上。因此，预激变压器的二次端电压V2t将领先于主变压器的二次端电压V2m。为了使每个变压器中的磁通量相同，每匝电压应相同。为了使主变压器和预激变压器一次绕组的每匝电压相同，预激变压器一次绕组的匝数应为
$$\mathrm{RD绕组匝数,\:𝑁_{𝑅𝐷 }=\frac{√3}{2}𝑁_{𝑃}}$$
然后，
$$\mathrm{\frac{𝑉_{2𝑡}}{𝑁_{𝑆}}=\frac{𝑉_{𝑅𝐷}}{𝑁_{𝑅𝐷}}}$$
$$\mathrm{\Rightarrow\:𝑉_{2𝑡} =\frac{𝑁_{𝑆}}{𝑁_{𝑅𝐷}}𝑉_{𝑅𝐷} =(\frac{𝑁_{𝑆}}{\frac{√3}{2}𝑁_{𝑃}})(\frac{√3}{2}𝑉_{𝐿})}$$
$$\mathrm{\Rightarrow\:𝑉_{2𝑡} =\frac{𝑁_{𝑆}}{𝑁_{𝑃}}𝑉_{𝐿} = 𝑉_{2𝑚} … (3)}$$
因此，主变压器和预激变压器的二次绕组在幅值上具有相同的电压，但它们在时间上相差90°，从而产生平衡的两相系统。
输入和输出电流之间的关系
设IR、IY和IB为三相输入侧的线电流。
$$\mathrm{𝐼_{1𝑚} = 主变压器的一次电流}$$
$$\mathrm{𝐼_{2𝑚} = 主变压器的二次电流}$$
$$\mathrm{𝐼_{1𝑡} = 预激变压器的一次电流}$$
$$\mathrm{𝐼_{2𝑡} = 预激变压器的二次电流}$$
现在，从连接图中，
$$\mathrm{𝐼_{1𝑡} = 𝐼_{𝑅}}$$
由于两个变压器的二次绕组相同，因此，
$$\mathrm{|𝐼_{2𝑚}| = |𝐼_{2𝑡}| = 𝐼_{2}\:(假设)}$$
如果忽略变压器的励磁电流，则预激变压器的磁势平衡方程由下式给出：
$$\mathrm{𝐼_{1𝑡}𝑁_{𝑅𝐷} = 𝐼_{2𝑡}𝑁_{𝑆}}$$
$$\mathrm{\Rightarrow\:𝐼_{𝑅}(\frac{√3}{2}𝑁_{p})}=𝐼_{2𝑡}𝑁_{𝑆}$$
所以，
$$\mathrm{𝐼_{𝑅} = 𝐼_{1𝑡} =\frac{2}{√3}(\frac{𝑁_{𝑆}}{𝑁_{𝑃}})𝐼_{2𝑡} = 1.15\:𝐾\:𝐼_{2𝑡}\:\: … (4)}$$
其中，𝐾 =$(\frac{𝑁_{𝑆}}{𝑁_{𝑃}})$是变压器的变比。所以，
$$\mathrm{𝐼_{2𝑡} =\frac{2}{√3}(\frac{𝐼_{𝑅}}{𝐾})}\:… (5)$$
现在，主变压器的磁势平衡方程为：
$$\mathrm{𝐼_{1𝑚}𝑁_{𝑌𝐷} − 𝐼_{1𝑚}𝑁_{𝐵𝐷} = 𝐼_{2𝑚}𝑁_{𝑆}}$$
$$\mathrm{\Rightarrow\:𝐼_{𝑌}(\frac{𝑁_{𝑃}}{2})− 𝐼_{𝐵}(\frac{𝑁_{𝑃}}{2})= 𝐼_{2𝑚}𝑁_{𝑆}}$$
$$\mathrm{\Rightarrow\: 𝐼_{𝑌} − 𝐼_{𝐵} = 2(\frac{𝑁_{𝑆}}{𝑁_{𝑃}})𝐼_{2𝑚} = 2\:𝐾\:𝐼_{2𝑚}\:… (6)}$$
所以，
$$\mathrm{𝐼_{2𝑚} =\frac{1}{2}({\frac{𝐼_{𝑌} − 𝐼_{𝐵}}{𝐾}})\:\:… (7)}$$
现在，对于平衡三相系统，
$$\mathrm{𝐼_{𝑅} + 𝐼_{𝑌} + 𝐼_{𝐵} = 0}$$
$$\mathrm{∴\: 𝐼_{𝐵} = −𝐼_{𝑅} − 𝐼_{𝑌}\: … (8)}$$
将IB的值代入方程（6），得到：
$$\mathrm{𝐼_{𝑌} − (−𝐼_{𝑅} − 𝐼_{𝑌}) = 2\:𝐾\:𝐼_{2𝑚}}$$
$$\mathrm{\Rightarrow\: 2𝐼_{𝑌} + 𝐼_{𝑅} = 2\:𝐾 \:𝐼_{2𝑚}}$$
$$\mathrm{\Rightarrow\:𝐼_{𝑌} = −\frac{𝐼_{𝑅}}{2}+ 𝐾\: 𝐼_{2𝑚} … (9)}$$
再次将电流IY的值代入等式（8），得到：
$$\mathrm{𝐼_{𝐵} = −𝐼_{𝑅} −(-\frac{𝐼_{𝑅}}{2})+ 𝐾 \:𝐼_{2𝑚})}$$
$$\mathrm{\Rightarrow\:𝐼_{𝐵} = −\frac{𝐼_{𝑅}}{2}− 𝐾 \:𝐼_{2𝑚} … (10)}$$
这些电流方程适用于平衡负载和非平衡负载。
Scott-T连接的应用
变压器的Scott连接用于以下应用：
Scott连接用于连接三相系统和两相系统，并允许功率在两个方向流动。
当从三相电源获取电源时，它用于同时操作两个单相电炉。
它还用于从平衡三相电源为单相负载（如电力机车）供电。
9K+浏览量
