数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究编译器设计中的搜索树和哈希表是什么？
搜索树
一种更有效的符号表组织技术是在每个记录中添加两个链接字段 LEFT 和 RIGHT。我们使用这些字段将记录链接到二叉搜索树中。
这棵树具有以下属性：通过跟随链接 LEFT (i)，然后跟随任何链接序列，从 NAME (i) 可访问的所有名称 NAME (j) 在字母顺序中都位于 NAME (i) 之前（符号表示，NAME (j) < NAME (i)）。
类似地，从 RIGHT (i) 开始访问的所有名称 NAME (k) 都将具有 NAME (i) < NAME (k) 的属性。因此，如果我们正在搜索 NAME 并找到了 NAME (i) 的记录，我们只需要在 NAME < NAME (i) 时跟随 LEFT (i)，并且只需要在 NAME (i) < NAME 时跟随 RIGHT (i)，当然，如果 NAME = NAME(i)，我们就找到了我们正在寻找的内容。
二叉搜索树算法
- 最初，Ptr 将指向树的根节点。
- 当 Ptr ≠ NULL 时执行以下操作
- 如果 NAME = NAME (Ptr)
- 则返回 true
- 否则如果 NAME<NAME (Ptr) 则
- Ptr−= LEFT(Ptr)
- 否则 Ptr−= RIGHT (Ptr)
- 循环结束
复杂度
如果以随机顺序遇到名称，则树中路径的平均长度将与 log n 成正比，其中 n 是名称的数量。因此，每次搜索都遵循从根节点开始的一条路径，输入 n 个名称并进行 m 次查询所需的时间预计与 (n + m) log n 成正比。如果 n 大于约 50，则二叉搜索树相对于链接列表以及可能相对于链接自组织列表具有明显的优势。
哈希表
哈希是一种用于搜索符号表记录的重要过程。此方法优于列表组织。
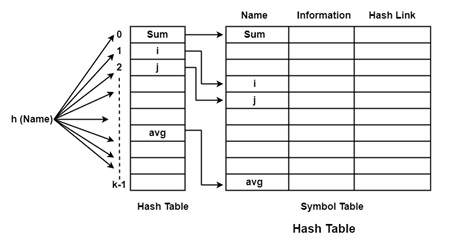
在哈希方案中，维护两个表
- 哈希表
- 符号表
哈希表包含从 0 到 K − 1 的 K 个条目。这些条目是指向符号表的指针，指向符号表的名称。它可以确定“名称”是否在符号表中，我们使用一个哈希函数'h'，包括 h (Name) 将导致一个介于 0 到 K − 1 之间的整数。我们可以通过 position = h(Name) 搜索任何名称。
使用此位置，我们可以访问符号表中名称的确切位置。
哈希函数应导致名称在符号表中的分布。哈希函数应确保碰撞次数最少。碰撞是指哈希函数导致存储名称的相同位置的情况。有多种碰撞解决技术，例如开放寻址、链接和重新哈希。
复杂度
此方案能够在与 n(n + m)/k 成正比的时间内对 n 个名称执行 m 次访问，其中 k 是我们选择的任何常数。由于 k 可以根据需要设置得足够大。这种方法通常优于线性列表或搜索树，并且在大多数情况下是符号表的首选技术，尤其是在存储空间不是特别昂贵的情况下。
2K+ 次浏览
