BCD 的全称是什么？

---

（BCD）的定义和解释

将十进制整数转换为其二进制等价物的一种技术称为二进制编码十进制 (BCD)。

• 一组位用于表示每个十进制数字

• 您可以为此编码使用 4 位或 8 位。

• 与现有的二进制系统相比，它是一种快速有效的方法，可以将输入值转换为二进制数字。

• 在难以更改数据的数字显示器中，它们经常被使用。

• 由于在这种情况下每个数字都作为单独的单个子电路进行控制，因此 BCD 绝对必不可少。

数字和小数部分中每个十进制数字的 BCD 等价物是其四位二进制值。8421 BCD 代码是 BCD 代码的另一个名称。从 MSB 到 LSB，四位组中不同位的权重由数字 8、4、2 和 1 表示。

当以二进制编码时，一些十进制数字具有无限位值，而它们在十进制中仅具有有限位值。数字 0.2 的二进制表示为 .001100，BCD 表示为 0.0010。

仔细观察下表如何描述这一点 -

示例：(321)10 的 BCD 转换

根据上表，

3 = 0011

2 = 0010

1 = 0001

因此，BCD = 0011 0010 0001

BCD 和数字系统：目的和用途

称为“二进制编码十进制”的4 位二进制整数专门用于表示十进制数。

用途

在数字系统中使用二进制编码十进制来表示十进制值的根本好处在于它在十进制和二进制表示之间转换的简单性。二进制编码十进制 (BCD) 中的每个十进制数字都由一个四位数表示，并且每个数字也可以表示为二进制值的加权和。

BCD 和计算机科学：应用和示例

BCD 或二进制编码十进制是数字 0 到 9 的四位二进制表示，通常称为“分组十进制”。一些早期的十进制计算机（例如 IBM System/360 系列）使用 BCD。它用于添加 BCD 数字。对于 BCD 数字，有 10 种替代的四位表示。

数字逻辑中的 BCD 加法器

假设 A 和 B 是四位数。A 和 B 的十进制整数的值可以从 0（二进制为 0000）到 9（二进制为 1001）。如果忽略前一个总和的进位，则输出范围将为 0 到 18。因此，如果考虑进位，则输出将具有最大值为 19（9 + 9 + 1 = 19）。当我们只添加 A 和 B 时，我们会得到二进制和。在这种情况下，我们将使用BCD 加法器以 BCD 格式获取结果。

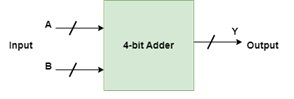
数字逻辑中 BCD 加法器的表示

说明：插图描绘了 BCD 在计算机科学中的使用

示例 -

输入：A = 0101 B = 1001

输出： Y = 1 0100

解释：正在添加两个数字 A（= 5）和 B（= 9）。

1110（= 14）将是二进制和的值。

但是由于 1 的二进制值为 0001，4 的二进制值为 0100，因此 BCD 和将为 1 0100。

BCD 和数据存储：优点和缺点

优点

二进制编码十进制对于数字显示器很有用，在数字显示器中，处理或显示大数字可能很困难。二进制编码十进制将每个数字视为一个单独的子电路这一事实使得更容易管理此类设备中的数据。在此类面板上，可以配置集成电路以产生二进制编码十进制数字。

缺点

除了优点之外，二进制编码十进制还具有一些缺点。将十进制数编码为二进制编码十进制会浪费计算机内存中的空间，并且是存储数字的低效方式。此外，与传统的二进制系统相比，它需要更复杂的电路。二进制编码十进制编码也可能造成浪费，因为许多 4 位状态（10 到 16）效率低下。

结论

在二进制编码十进制中，基数 10 整数的每个数字都由一组四个二进制数字或位表示。使用二进制编码十进制时，可以以二进制格式显示每个基数 10 数字或数字。很明显，所有 BCD 做的只是为每个十进制数字提供二进制表示。指定的十进制值更重，并且在 BCD 表示中需要更多位。

常见问题

Q1. BCD 有哪些类型？

答：二进制编码十进制有两种类型。

非压缩 BCD

在计算机上，非压缩二进制编码十进制数的每个 4 位组都存储在其自己的寄存器中。如果寄存器为 8 位或更宽，则这具有使用更少的存储空间来存储二进制编码十进制整数的缺点。

压缩 BCD

两个二进制编码十进制数字被打包到一个 8 位寄存器中作为值。可以通过将较高寄存器中的数字向左移动四次，然后组合上下寄存器中的数字，在一个寄存器中存储两个二进制编码十进制数字。

Q2. BCD 和简单的二进制表示有什么区别？

答：在简单的二进制表示中，整个数字被重复除以 2 以创建其二进制形式。在二进制编码十进制中，每个单独的数字都转换为二进制。然后将每个数字转换为其 4 位二进制对应项，然后再组合。

这是一个例子

十进制形式的 234。

234 的二进制表示为：11101010

234 以二进制编码十进制表示如下

2 = 0010, 3 = 0011, 4 = 0100

因此，234 = 001000110100

Q3. (4589)10 的 BCD 表示是什么？

答：(4589)10 的 BCD 转换

根据上表，

4 = 0100

5 = 0101

8 = 1000

9 = 1001

因此，BCD = 0100010110001001