数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究什么是编译器设计中的自顶向下回溯分析？
在自顶向下回溯分析中，分析器将尝试使用多个规则或产生式来识别输入字符串的匹配项，并在推导的每一步都进行回溯。因此，如果应用的产生式没有得到所需的输入字符串，或者与所需的字符串不匹配，则可以撤消该移位。
示例 1 - 考虑以下语法
S → a A d
A → b c | b
为字符串 a bd 创建语法树。此外，当选择错误的备选方案时，显示需要回溯时的语法树。
解决方案
字符串 abd 的推导将是 -
S ⇒ a A d ⇒ abd（所需字符串）
如果将bc替换为非终结符 A，则获得的字符串将是 abcd。
S ⇒ a A d ⇒ abcd（错误的备选方案）
图 (a) 表示 S → aAd
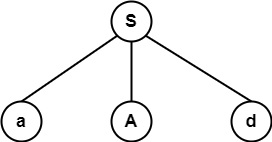
图 (b) 表示使用产生式 A → bc 扩展树，该产生式生成字符串 abcd，该字符串与字符串 abd 不匹配。因此，它回溯并选择另一个备选方案，即图 (c) 中的 A → b，该方案与 abd 匹配。
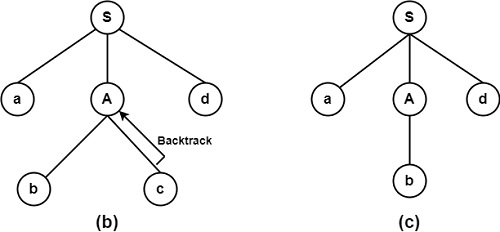
回溯算法
示例 2 - 为以下语法的自顶向下回溯分析编写算法。
S → a A d
A → bc| b
解决方案
在以下算法中，每个非终结符 S 和 A 都有一个过程。语法中的终结符 a、b、c、d 是分析器要读取的输入符号或前瞻符号。
advance( ) - 它是一个用于将输入指针移动到下一个输入符号的函数。
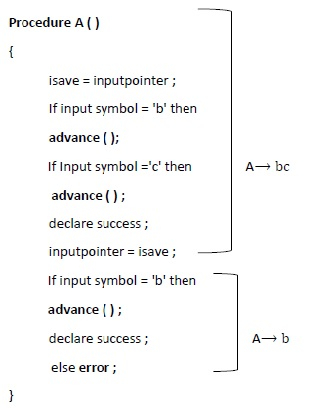
自顶向下回溯分析的局限性
以下是自顶向下回溯分析中出现的一些问题。
回溯 - 回溯看起来非常简单易于实现，但选择不同的备选方案会导致很多问题，如下所示 -
撤消语义操作需要大量开销。
在分析期间在符号表中创建的条目必须在回溯时删除。
由于这些原因，回溯不用于实际编译器。
左递归 - 如果语法具有以下形式的产生式，则该语法是左递归的。
A → Aα|β
这会导致分析器进入无限循环。
选择正确的产生式 - 测试备选方案的顺序可以改变接受的语言。
难以定位错误 - 发生故障时，很难知道错误发生在哪里。
8K+ 次浏览
