渐近符号

渐近符号

渐近符号用来表示算法的复杂度用于渐近分析。 这些符号是用于表示复杂度的数学工具。 一般来说使用三种符号。

大 O 符号

大 O（O）符号给出了到某一常数因子的函数 f(n) 的上限。

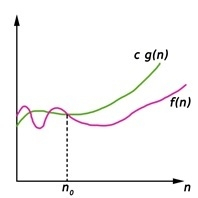
我们写出 f(n) = O(g(n))，如果正数常数 n0 和 c 存在，对于大于 n0 的数，f(n) 总是落在 c*g(n) 上或其下方。

O(g(n)) = { f(n) : 存在正数常数 c 和 n0，对于大于或等于 n0 的任何 n，0 ≤ f(n) ≤ c g(n)}

大 Ω 符号

大 Ω（Ω）符号给出了到某一常数因子的函数 f(n) 的下限。

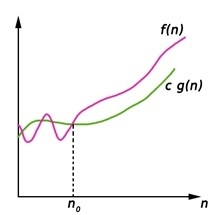
我们写出 f(n) = Ω(g(n))，如果正数常数 n0 和 c 存在，对于大于 n0 的数，f(n) 总是落在 c*g(n) 上或其上方。

Ω(g(n)) = { f(n) : 存在正数常数 c 和 n0，对于大于或等于 n0 的任何 n，0 ≤ c g(n) ≤ f(n)}

大 Θ 符号

大Θ(Θ) 符号标注法能给出函数 f(n) 范围的一个常量因子。

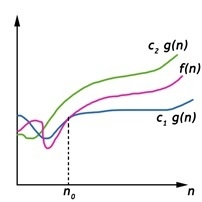
如果存在正数 n0 和 c1 以及 c2，使得在 n0 右侧的 f(n) 时刻处于 c1*g(n) 与 c2*g(n) 之间（含）的话，我们写为 f(n) = Θ(g(n))。

 Θ(g(n)) = {f(n) : 存在正数 c1、c2 和 n0，使得对于所有 n ≥ n0，均有 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n)}

更新于: 2023 年 10 月 21 日

29K+ 浏览量

启动您的职业

完成课程即可获得认证

开始学习
广告