两个n位二进制数的加法

---

在数字电子学和数字系统（如数字计算机、计算器等）中，二进制数及其算术运算起着至关重要的作用。与十进制数系统一样，我们也可以对二进制数执行所有四种基本算术运算，即二进制数的加法、减法、乘法和除法。阅读本文，了解如何添加两个n位二进制数。

什么是二进制加法？

二进制加法是在二进制数上执行的基本算术运算，其中将任意位数的两个二进制数相加以获得和。

众所周知，二进制数系统基数为二，仅包含两个符号或数字，即0和1。因此，两个二进制数的加法类似于十进制数的加法，只是系统的基数为2。在讨论二进制加法过程之前，让我们了解一下二进制加法的规则。

二进制加法的规则

我们必须遵循布尔代数的某些规则才能执行两个二进制数的二进制加法。执行二进制加法需要遵循四个规则。这些规则如下所示：

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 0 (进位1)

因此，当添加前三组位时，不会产生进位。但是，当添加两个1位时，和位为0，并产生进位位1。

现在，让我们通过示例来了解两个二进制数的加法。

示例

将两个3位二进制数111和101相加。

解答

给定的二进制数为111和101。我们可以如下添加这两个3位二进制数：

	第3列	第2列	第1列
来自先前加法的进位	1	1	无进位
第一个二进制数	1	1	1
第二个二进制数	1	0	1
和位	1	0	0
进位位	1	1	1

因此，此二进制加法的结果是：

111 + 101 = 1100

此二进制加法的系统表示如图1所示。

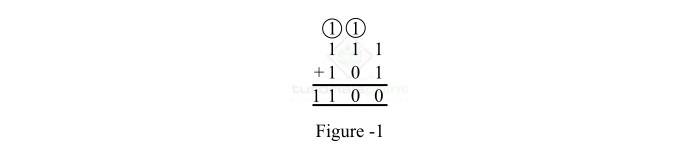
解释

二进制数111和101的二进制加法按照以下步骤执行：

• 步骤1 - 首先，我们考虑第1列，并添加第1列的位，即(1+1)，根据二进制加法的规则，它给出和位0和进位位1。和位保留在第1列中，进位位1被转发到第2列。

• 步骤2 - 在第2列中，我们添加1+(1+0)。它给出和位0（保留在第2列中）和进位位1，该位被转发到下一列。

• 步骤3 - 在第3列中，我们添加1+(1+1)。它给出和位1和进位位1。

最后，记录和结果，即1100。

了解了特定位数的二进制加法后，我们可以将其扩展到任意位数。

两个n位二进制数的加法

上述示例中遵循的二进制加法过程可以推广到任何两个n位二进制数。

我们可以按照以下步骤执行两个n位二进制数的加法：

假设有两个n位二进制数：

$$A=A_{n}\cdot \cdot \cdot A_{3}A_{2}A_{1}$$

$$B=B_{n}\cdot \cdot \cdot B_{3}B_{2}B_{1}$$

现在，让我们添加这两个二进制数。

	第n列	第3列	第2列	第1列
来自先前加法的进位	C(n-1)	C2	C1	无进位
第一个二进制数	An	A3	A2	A1
第二个二进制数	Bn	B3	B2	B1
和位	Sn = An + Bn + C(n-1)	S3 = A3 + B3 + C2	S2 = A2 + B2 + C1	S1 = A1 + B1
进位位	Cn	C3	C2	C1

这两个n位二进制数的二进制加法的结果将是：

$$S=C_{n}S_{n}\cdot \cdot \cdot S_{3}S_{2}S_{1}$$

此加法也可以用图2所示的标准布局表示。

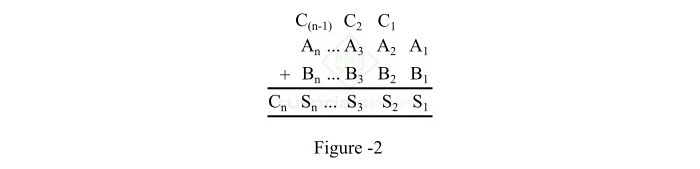
解释 - 两个n位二进制数的二进制加法按照以下步骤执行：

• 步骤1 - 首先，考虑第1列，并添加第1列的位，即(A₁ + B₁)。它给出和位S₁和进位位C₁作为结果。

• 步骤2 - 将和位S₁保留在第1列中，并将进位位C₁转发到第2列。

• 步骤3 - 现在，添加第2列的位，即(C₁ + A₂ + B₂)。它给出和位S₂和进位位C2。将和位S₂保留在第2列中，并将进位位移动到第3列。

• 步骤4 - 以相同的方式对每一列执行加法。

• 步骤5 - 在第n列中，我们添加(C_(n-1) + A_n + B_n)。它给出和位S_n和进位位C_n。

最后，将所有结果位组合在一起，以获得给定n位二进制数的和，如下所示：

$$S=C_{\left ( n-1 \right )}S_{n}\cdot \cdot \cdot S_{3}S_{2}S_{1}$$

这就是两个n位二进制数加法的最终结果。

这就是关于两个n位二进制数加法的全部内容。为了精通二进制数的加法，请尝试解决以下教程问题。

问1 - 将两个5位二进制数11011和10110相加。

问2 - 将这两个二进制数相加：1011 + 1101。

问3 - 将这两个二进制数相加：1110011和1011011。

问4 - 执行加法：10111 + 10011。

问5 - 将这两个二进制数相加：1111 + 1001。