安培环路定律及其应用

---

介绍

安培定律为电动力学的发展树立了里程碑。1920 年，汉斯·奥斯特用指南针和载流导线进行了一次经典实验。他观察到，如果导线中没有电流，则指南针始终指向北极。然而，在导线中有电流的情况下，指针会向某个方向偏转。他发现偏转方向与圆相切，即磁场方向（图 1）。

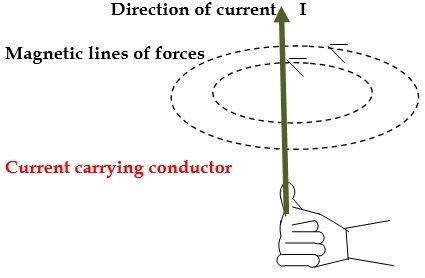
图 1：载流导线周围的磁场方向

这表明载流导线在其周围产生磁场。原则上，我们总是可以使用毕奥-萨伐尔定律来估计载流导线产生的磁场。为了估计任何电流分布产生的净磁场，我们首先写出微分磁场 (dB) ⃗，然后将其在整个分布上求和。但是，如果我们的电流分布存在对称性呢？我们能否简化计算？答案是肯定的。安培定律帮助我们计算磁场。

安德烈-玛丽·安培是谁？

安德烈-玛丽·安培出生于 1775 年，是一位法国物理学家和数学家。他是一位神童，12 岁就开始学习数学。奥斯特发现电流产生磁场，这吸引了他对该领域的兴趣。他继承了奥斯特的工作，并证明了载流导线相互排斥或吸引。这种排斥或吸引取决于导线中电流的方向。他因其著名的成果“安培定律”而闻名。为了纪念他，电流的 SI 单位以他的名字命名。

安培环路定律的表述

安培定律可以这样表述：“穿过任何闭合回路的磁场力的线积分与穿过该回路的电流成正比。”

如果有多个电流穿过回路，我们将取回路包围的电流的数值和。用于计算的回路称为“安培回路”或“安培线圈”。

安培环路定律的另一种形式

假设存在一个闭合路径 C，并且穿过它的净电流为 $\mathrm{i_{enc}}$，则

$$\mathrm{\int \overrightarrow{B}.\overrightarrow{dl}=\mu_0i_{enc}}$$

让我们分析这个方程式的每一项。

$\mathrm{\overrightarrow{B}}$ 的线积分 - 我们可以将回路分成小的矢量元素 $\mathrm{\overrightarrow{dl}}$。然后

$$\mathrm{\overrightarrow{B}.\overrightarrow{dl}=Bdl\:cos\theta}$$

因此，它是线元素和磁场切向部分（Bcosθ）的乘积。回路。

净电流 $\mathrm{i_{enc}}$ - 我们需要考虑仅穿过回路的电流元素的代数和。

从图中，只有 $\mathrm{i_{enc}=i_1+i_2}$

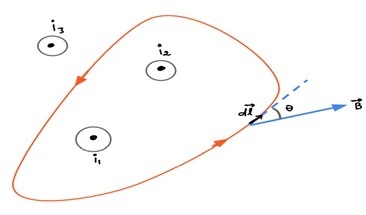
积分方向 - 可以使用右手定则计算积分方向。如果我们弯曲右手，使手指指向积分方向，则伸出的拇指将指向电流的正方向。

安培环路定律的不一致性

让我们将安培定律应用于下图所示的情况。我们有一个电容器，传导（常规）电流用 $\mathrm{i_c}$ 表示。根据安培定律，路径周围的积分 $\mathrm{\overrightarrow{B}.\overrightarrow{dl}}$ 应该等于 $\mathrm{μ_0 i_{enc}}$

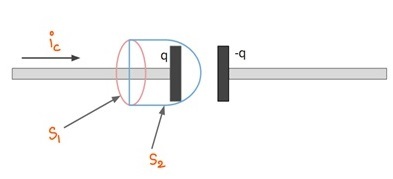
这里我们取两个表面。对于表面 $\mathrm{S_1:i_{enc}=i_c}$

对于向右凸出的表面 $\mathrm{S_2}$：$\mathrm{i_{enc} = 0}$，因为电容器间隙之间不存在电流。

这里 $\mathrm{\overrightarrow{B}.\overrightarrow{dl}}$ 为零，而 $\mathrm{i_c}$ 同时为同一路径，这与矛盾。

修正的安培环路定律或安培-麦克斯韦环路定律

麦克斯韦通过引入一个称为“位移电流”的新项来修改安培定律，以消除这种歧义。它被定义为

$$\mathrm{i_d=\epsilon_0\:\frac{d\Phi_E}{dt}}$$

其中 $\mathrm{\Phi_E}$ 是通过表面的电通量，由 $\mathrm{\Phi_E=\int \overrightarrow{E}.\overrightarrow{dA}}$ 给出。

因此，安培定律或安培-麦克斯韦定律的修正形式为 -

$$\mathrm{\int (\overrightarrow{B}).(\overrightarrow{dl})=\mu_0(i_c+i_d)=\mu_0i_c+\mu_0 \epsilon_0 \frac{d\Phi_E}{dt}}$$

现在我们可以使用安培-麦克斯韦定律来解决电容器情况下出现的问题。

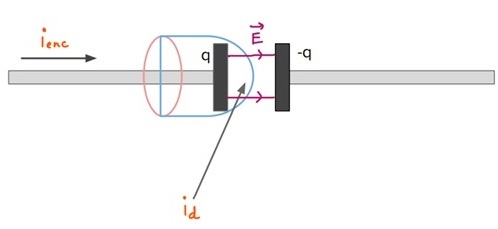
如果我们将此定律应用于表面 $\mathrm{S_1:i_{enc}=i_c}$，则与往常一样

但是对于向右凸出的表面 $\mathrm{S_2}$：$\mathrm{i_{enc} = 0}$，但 $\mathrm{i_d= \epsilon_0 \frac{d\Phi_E}{dt}}$，因为电容器间隙之间的电场将是可变的。

因此，如果回路内部存在时变场，我们必须使用安培-麦克斯韦定律来解决问题。

安培环路定律的应用

我们可以将安培定律用于电流分布对称的各种问题。

让我们考虑一根半径为 R 的直导线，它承载电流 i。让我们应用安培定律来估计该导线在距离 r 处的磁场。(r>>R)

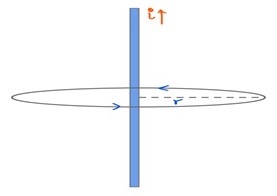
我们可以看到导线具有圆柱对称性。使用右手定则，我们可以计算 B 的方向。它出现在安培回路的每个点的切线上，线元素dl与安培回路平行。这意味着 $\mathrm{\overrightarrow{B}}$ 和 $\mathrm{\overrightarrow{dl}}$彼此平行。

这意味着

$$\mathrm{\overrightarrow{B}.\overrightarrow{dl}=Bdl\:cos\theta = B\:dl\:cos\:0^{\circ}=Bdl}$$

安培定律

$$\mathrm{\int\overrightarrow{B}.\overrightarrow{dl}=\oint B.dl=B\:\oint\:dl=B.2\Pi r = \mu_0 I}$$

因此

$$\mathrm{B =\frac{\mu_0 i}{2\pi r}}$$

这是一个众所周知的结果，也可以使用毕奥-萨伐尔定律进行验证。

解题示例

示例 1：求表面 1 和 2 中 $\mathrm{\overrightarrow{B}.\overrightarrow{dl}}$ 的值。

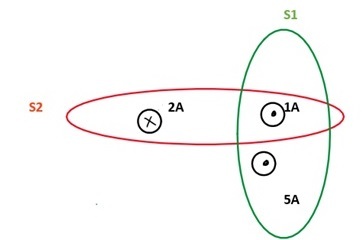
答：我们可以从图中看到 S1 包含两个电流 1A 和 $\mathrm{5A.\overrightarrow{B}.\overrightarrow{dl} =6}$ S2 也包含两个电流，但其中一个方向相反。$\mathrm{\overrightarrow{B}.\overrightarrow{dl}=5-2=3}$

示例 2：一根半径 R=2cm 的长直导线承载 10A 的电流。求其 8cm 处的磁场？

我们已经推导出直导线磁场的方程式。我们可以在此处直接使用它。

$$\mathrm{B =\frac{\mu_0 i}{2\Pi r}=\frac{4\Pi\times 10^7\times10}{2\Pi\times 8 \times10^{−2}}=\frac{20\times 10^{−5}}{8}=2.5\times 10^{−5}\:Tesla}$$

结论

我们可以使用安培定律简化对电流分布产生的磁场的估计。但只有在系统存在某种对称性时才能使用它。如果回路内部存在某些时变电场源，则安培定律无法给出任何合理的结果。麦克斯韦针对此类情况修改了该定律，并引入了位移电流的概念。这可以用电容器的情况来证明。我们可以使用安培定律来估计载流直导线产生的磁场，结果表明它与我们计算磁场的距离成反比。

常见问题

Q1. 写出除载流导线之外的磁场源？

答：变化的电场也可以产生磁场

Q2. 安培定律在回路中是否适用于所有类型的电流？

答：否，这些仅适用于稳恒电流。

Q3. 我们可以从安培定律推导出毕奥-萨伐尔定律吗？

答：是的，它们可以相互推导。

Q4. 静电学中相当于安培定律的是什么？

答：高斯定律相当于安培定律。

Q5. 安培-麦克斯韦定律的结论是什么？

答：安培-麦克斯韦定律告诉我们，磁场可以通过载流导线以及变化的电场产生。