布拉格定律 - 定义、推导、公式、应用

---

简介

布拉格定律是原子和分子物理学中的一个重要概念。您已经知道原子是构成这个宇宙的基本单元。它们是宇宙中每一块物质的基础。但这并不是我们对微观世界了解的全部。事实上，我们甚至设法将原子分解成电子、质子和中子。如果这还不足以满足您的好奇心，您应该知道我们甚至了解“构成”电子和核子的东西。但我不再赘述了。

现在，让我们讨论一下原子的排列方式。在材料内部，原子或分子驻留在特定位置，并且最常见的是，在其排列中具有一定的周期性。此外，不同的材料具有不同的原子排列。

为了研究这些原子的位置，我们将晶体建模为一组离散的平行平面，原子驻留在这些平面上。这些平面应该是等距的。根据平行平面对晶体进行建模，使我们能够对晶体进行X 射线衍射研究。这些研究基于布拉格定律。让我们详细讨论一下。

布拉格定律？

在下图中，查看两个平行平面，它们之间距离为 d，波长为 λ的 X 射线辐射以角度 θ入射。

布拉格定律指出，从晶体中平行平面反射的波观察到的衍射图样将在满足以下条件时达到最大值：

$$\mathrm{2d\:sin\:θ =n\lambda}$$

这是一个非常简单但功能强大的方程，它构成了大量晶体学研究的基础。请注意，由于晶面间距(d)的数量级为几个埃，因此最适合晶体学研究的波长位于X 射线区域。

布拉格方程

布拉格方程指的是布拉格定律的数学表述。它最常见的形式写成如下：

$$\mathrm{2d\:sin\:θ =n\lambda}$$

这里，d 是晶面间距，θ 是入射角，λ 是入射辐射的波长。最后，n 是一个正整数，对应于衍射级数。

布拉格定律的另一种表述是用倒格子矢量 G 和入射波矢 k 表示，如下所示：

$$\mathrm{2 k.G+G^2= 0}$$

以上两个表述是相同的，但第二个是在倒空间中定义的。

布拉格定律的推导

布拉格定律可以用光学的非常简单的规则推导出来。请查看下面的图表：

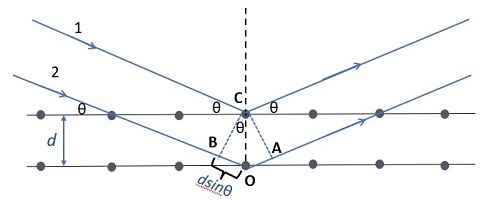
在这个图中，我们绘制了三个垂线，如下所示：

• OC 垂直于上面显示的两个平面。

• BC 垂直于入射光线。

• CA 垂直于反射光线。

从几何学上，我们可以证明$\mathrm{\angle BCO = \theta}$。现在，使用三角函数：

$$\mathrm{sin θ =\frac{对边}{斜边}=\frac{BO}{CO}}$$

由于 CO = d，我们有：

$$\mathrm{dsin\:\theta =BO}$$

此外，ΔCBO 和 ΔCAO 可以证明是全等的，因为它们共享一个公共斜边并具有两组相等的角。因此，BO = AO。光线 1 和 2 之间的光程差由BO + AO给出。也就是说，光程差$\mathrm{\delta}$为：

$$\mathrm{\delta=2BO=2d\:sin\:\theta}$$

为了使最大值发生，光程差必须是波长的整数倍。因此，我们得到布拉格条件如下：

$$\mathrm{2d\:sin\:\theta =n\lambda}$$

布拉格定律的应用

布拉格定律在晶体学领域有着广泛的应用。请看：

• 劳厄法、粉末晶体法和旋转晶体法等 X 射线衍射研究都基于布拉格定律。

• X 射线荧光光谱法基于布拉格定律的概念。

布拉格定律的重要性

术语布拉格衍射用于指当电磁辐射（基本上是光）从晶体学平面反射时观察到的衍射现象。只有当辐射的波长与晶面间距相当（发生在 X 射线区域）时，才会发生衍射。

布拉格衍射在非常特定的参数集中观察到。为了进行衍射研究，我们需要最大限度地提高这些参数满足的可能性。这是通过采用某些方法（如劳厄法、旋转晶体法等）来实现的。

示例

Q1：如果晶面间距为 2.014 埃，则计算二阶衍射的角度，给定波长为 1.544 埃。

答：布拉格定律给出$\mathrm{2d\:sin\:sin \:\theta =n\lambda}$

求解 theta

$$\mathrm{\theta=\frac{n\lambda}{2d}=\frac{2\times 1.544\times 10^{−10}}{2\times2.014\times 10^{−10}}=0.766666 =50.05^{\circ}}$$

Q2：给定一个晶面间距为 3.03 埃的晶体，求第一衍射极大的入射角。在这种情况下，入射中子束的能量为 0.1 eV。$\mathrm{(中子质量 = 1.67\times\:10^{−27}\:kg)}$。

答：第一步是根据给定的能量计算波长。我们使用德布罗意公式。

$$\mathrm{\lambda=\frac{h}{\sqrt{2mqE}}=\frac{6.626\times 10^{−34}}{\sqrt{2×1.67\times 10^{−27}\times 1.6\times10^{−19}\times0.1}}=9.06\times 10^{−11}m}$$

接下来，我们使用布拉格定律来求解 θ

$$\mathrm{2d\:sin\:sin\:\theta =n\lambda}$$

$$\mathrm{\theta=\frac{n\lambda}{2d}=\frac{9.06\times 10^{−11}}{2\times 3.03\times 10^{−10}}=0.1495 =8.59^{\circ}}$$

因此，入射角必须为$\mathrm{8.59^{\circ}}$

结论

X 射线衍射是表征固体晶体的重要技术。这些衍射研究基于布拉格定律，该定律将晶体建模为一组离散的平行平面，然后推导出晶面间距、入射角和入射辐射波长之间的关系。

假设晶面间距由 d 表示，入射角由 θ 表示，入射辐射的波长由 λ 表示。然后布拉格定律指出，只有当满足以下条件时，才会观察到衍射的最大值：

$$\mathrm{2d\:sin\:\theta =n\lambda}$$

布拉格定律的推导涉及几何光学的简单定律。布拉格衍射（指由于电磁辐射被晶体平面反射而观察到的衍射）用于晶体的 X 射线衍射和 X 射线荧光光谱法。

常见问题

Q1. 所有晶体是否都允许所有晶面发生衍射？

答：否。不同类型的晶体具有不同的原子排列方式。因此，在一个类型的晶体中允许衍射的平面可能在其他晶体中不会发生衍射。例如，面心晶体仅当所涉及平面的米勒指数全部为奇数或全部为偶数时才会显示衍射。

Q2. 布拉格定律中观察到哪种散射？

答：这里观察到瑞利散射，因为波长没有发生变化。

Q3. 单个晶体是否可以具有多个晶面间距值？

答：是的。晶体中存在不同的平行平面组。这些平面以它们的米勒指数 h、k 和 l 为特征。晶面间距的值取决于米勒指数。

Q4. 典型的 X 射线衍射光谱是什么样的？

答：X 射线衍射光谱绘制在以强度作为 2θ 函数的图上。通常，它在 θ 的特定值处显示几个峰，其余区域几乎是平坦的且为零。

Q5. 为什么 XRD 光谱以 2θ 而不是 θ 为单位绘制？

答：这与晶体衍射方法的设计方式有关。衍射的结果通过放置在晶体周围的探测器观察到。通常，衍射光束位于 2θ 角的圆锥体上。因此，XRD 光谱以 2θ 为单位绘制。

Q6. 为什么在晶体衍射中使用 X 射线？

答：大多数晶体的晶面间距的数量级与 X 射线的波长相似。如果波长与晶面间距有很大差异，则光将穿过晶体而不会发生衍射。因此，使用 X 射线。