布儒斯特角定律:定义、公式、示例
介绍
布儒斯特角定律是光学(光的科学)中研究的内容。如果光波能够完美地穿过所有材料,你将什么也看不到,所有材料都会变得隐形。另一方面,如果材料完美地反射所有光线,它们将始终呈现白色而不是彩色。颜色之所以可见,是因为材料吸收特定波长并反射其他波长。实际上,所有材料都选择性地反射、透射或吸收光线。
同时,具有特定特性的光波可以完全透射通过特定表面。这涉及到特定**偏振**的光以一定角度入射到表面上,然后被完全透射。首先,让我们了解什么是偏振。
如果你还记得,**光**是一种**电磁**波,因此包含电场和磁场。光线的电场分量振动的方向决定了它的偏振方向,简而言之,就是它的偏振。
什么是布儒斯特角定律?
当光入射到透明表面的边界时,反射和透射的光量取决于介质的**折射率**和入射波的偏振。布儒斯特角定律是一种关系式,它为我们提供了发生完全透射时的入射角。
示例:一块玻璃的**折射率**为1.5,如果放在空气中,**布儒斯特角**大约为56°。有趣的是,由于布儒斯特角取决于两种介质的折射率,因此空气到玻璃的布儒斯特角值将不同于水到玻璃的布儒斯特角值。
另一个需要注意的重要点是,当非偏振光以布儒斯特角入射时,反射分量在一个特定方向上是**完全偏振的**,而折射光线是部分偏振的。这使得我们可以通过反射产生特定方向偏振的光波。

Sobarwiki,布儒斯特角偏振,标记为公共领域,Wikimedia Commons 上有更多详细信息
布儒斯特角定律公式
如果我们分别用 $\mathrm{n_1}$ 和 $\mathrm{n_2}$ 表示第一种和第二种介质的**折射率**,则布儒斯特角由下式给出:
$$\mathrm{\theta_B=\arctan{\frac{n_2}{n_1}}}$$
回顾一下柯西关系。材料的折射率不是一个普遍常数,它本身是波长的函数。因此,不同波长的光的布儒斯特角是不同的。但是,对于可见光区域,布儒斯特角的变化很小。
布儒斯特角推导
可以使用斯涅耳定律得到布儒斯特角的一个简洁而简单的推导。
当来自折射率为 $\mathrm{n_1}$ 的材料的光以 $\mathrm{\theta_1}$ 角入射到折射率为 $\mathrm{n_2}$ 的材料上时,折射角 $\mathrm{\theta_2}$ 与这些量之间的关系为:
$$\mathrm{n_1\:sin\:\theta_1 =n_2\:sin \: \theta_2}$$
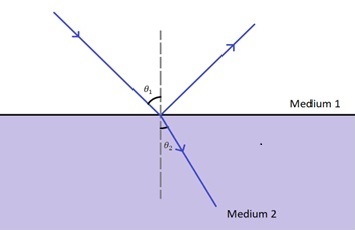
现在,事实证明,光波与介质的物理相互作用方式是,当 $\mathrm{\theta_2=90^{\circ}-\theta_1}$ 时,反射为零。因此,
$$\mathrm{n_1\:sin\:\theta_1 =n_2\:sin \: (90^{\circ}-\theta_1)}$$
$$\mathrm{\frac{sin\:\theta_1}{cos\: \theta_1}=\frac{n_2}{n_1}}$$
现在,正弦除以余弦就是正切。这里的 $\mathrm{θ_1}$ 就是布儒斯特角 $\mathrm{θ_B}$。因此,
$$\mathrm{tan\:\theta_B=\frac{n_2}{n_1}}$$
或者,
$$\mathrm{\theta_B=\arctan{\frac{n_2}{n_1}}}$$
可以使用麦克斯韦方程组、相关的边界条件和菲涅耳公式得到该关系式的更全面的证明。
布儒斯特角和临界角之间的关系
你一定还遇到过临界角的概念。两种介质界面的临界角定义为折射光线与法线成 $\mathrm{90^{\circ}}$ 角时的角度。也就是说,超过临界角,所有光线都会被反射,不会发生折射。这被称为全内反射。
临界角可以通过简单地应用斯涅耳定律来找到。如果 $\mathrm{\theta_C}$ 是临界角,则
$$\mathrm{n_1\:sin\:\theta_C =n_2\:sin\: 90^{\circ}=n_2}$$
因此,
$$\mathrm{sin\:\theta_C=\frac{n_2}{n_1}}$$
我们可以将右边的分数等同于布儒斯特角的正切。因此,
$$\mathrm{sin\:\theta_C=tan\:\theta_B}$$
这就是布儒斯特角和临界角之间的关系。
布儒斯特角定律的应用
布儒斯特角定律在各种情况下都有应用:
你一定听说过**偏光太阳镜**。这些太阳镜涂有特定折射率的薄膜,可以透过反射阻挡从表面反射的光线,从而减少眩光。
摄影师会在镜头前放置**偏振滤光镜**,减少来自水平表面(如水面)的眩光,并允许他们拍摄反射表面下的物体。例如,如果你看到过清晰地显示湖中鱼类和动植物的湖泊图像,它很可能就是通过偏振镜头拍摄的。
只能从一面看到而另一面反射的窗户是基于偏振的概念。
**全息图**是由光波的干涉记录的。如果发生不需要的反射,则会出现噪声。相反,用于记录全息图的激光束是偏振的,并且以布儒斯特角入射。这使得产生的全息图更清晰。
在研究不同材料的**光学特性**时,以布儒斯特角入射的光线将被完美透射,从而减少不需要的反射损耗。
结论
我们知道,没有哪种材料是光的完美反射体、吸收体或透射体。如果存在这样的材料,它们将是隐形的、完全白色的或黑色的。相反,光的部分总是被反射或吸收。特定偏振的光可以被完全透射。请注意,**光的偏振**是指其电场分量振动的方向。当特定方向偏振的光以一定角度入射到透明界面的边界时,不会吸收反射。这个角度称为布儒斯特角,这个角度和所涉及的两种材料的折射率之间的关系由布儒斯特角定律给出,其公式为
$$\mathrm{\theta_B=\arctan{\frac{n_2}{n_1}}}$$
由于折射率取决于波长,因此布儒斯特角对于入射到同一界面的不同波长的光线是不同的。此外,布儒斯特角可以与临界角联系起来,临界角是发生全内反射时的角度。
$$\mathrm{sin\:\theta_C =tan\:\theta_B}$$
布儒斯特角定律在许多情况下都有应用。偏光太阳镜、偏振滤光镜、单向透视窗和全息图记录只是一些布儒斯特角定律发挥作用的例子。
常见问题
Q1. 折射率是如何与波长相关的?
A1. 柯西方程给出了折射率与波长的关系。
$$\mathrm{n=A+\frac{B}{\lambda^2}+\frac{C}{\lambda^4}+.....}$$
这里,A、B 和 C 是常数,而 λ 是光的波长。
Q2. 当非偏振光以布儒斯特角入射到界面上时,哪个偏振方向会被反射?
A2. 垂直于入射面的偏振光波将被反射。这也被称为 s 偏振。
Q3. 非偏振光是什么意思?
A3. 非偏振光是由所有可能方向偏振的光波组成的。因此,没有偏振相当于 $\mathrm{360^{\circ}}$ 偏振。
Q4. 我们如何获得偏振光?
A4. 各种材料只允许特定偏振的光线通过。如果我们想获得特定方向偏振的光线,我们应该将这些材料放置在光束的路径上。还有许多其他方法可以获得偏振光。我们可以通过反射、散射甚至折射产生偏振光。
Q5. 偏振会影响光波的强度吗?
A5. 会影响。通过偏振器的光强度与入射光束 θ 的强度有关。当非偏振光通过偏振器时,其强度减半。


 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C语言编程
C语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP