范德华方程的推导

---

简介

范德华方程通常被称为真实气体或一摩尔气体的范德华方程，这些气体不遵循理想气体定律。根据理想气体定律，PV = nRT，其中P表示施加到气体上的外部或内部压力，V表示体积，n表示摩尔数。在这个公式中，T表示温度，R表示通用气体常数。

什么是范德华方程？

关于真实气体的范德华方程表示方程的状态。就真实气体而言，理想气体行为在温度的压力方面不遵循理想气体方程。可以通过绘制表示压力和体积曲线（等温线）相对关系的图表来研究理想气体在施加压力方面的推导，即波义耳定律。

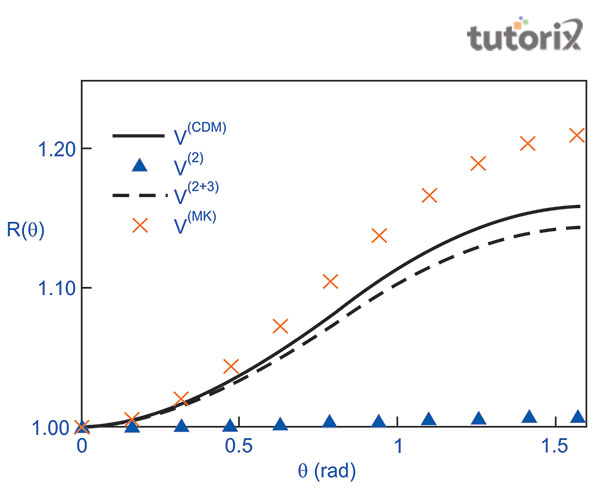
图1：范德华方程的对势相互作用

理想气体行为的可压缩因子用Z表示，可以用公式Z = PV/nRT表示。就理想气体而言，可压缩因子为1，但在真实气体的情况下，Z不等于1（Evarestov & Kuzmin，2020）。当Z的值大于1时，真实气体的推导为正，即Z>1，但当Z的值小于1时，真实气体的推导为负，即Z<1。

一摩尔气体的范德华方程的推导

根据气体定律，方程为PVm = RT，但根据范德华方程，它为C = Na/ Vm（Fedorov et al. 2018）。在这个公式中，主要作用于分子表面的净力有助于拉出容器，这与密度数成正比。

图2：一摩尔气体的范德华方程的推导

Atm lit² mol^-2 和 litre mol^-¹ 是范德华方程的单位。在低压下，影响此方程的可压缩因子也表示为(P + a/V²) ( V - b) = RT，但在大多数情况下，b被忽略，然后方程变为(P + a/V²) ( V) = RT。在高压情况下，可压缩因子通过方程(P + a/V² ) ( V - b) = RT表示，其中a/V²通常与压力相比被忽略，然后方程为(P) ( V - b) = RT

真实气体的范德华方程的推导

就真实气体而言，大多数情况下应用范德华气体方程。真实气体的体积主要表示为(Vm - b)，其中b被认为是一摩尔消耗的总体积（Kontogeorgis、Privat & Jaubert，2019）。真实气体的范德华气体方程为P(Vm - b) = nRT，其中V可以用Vm代替，即一摩尔气体的体积，r表示通用气体常数，T表示温度。

范德华方程在可压缩流体上的应用

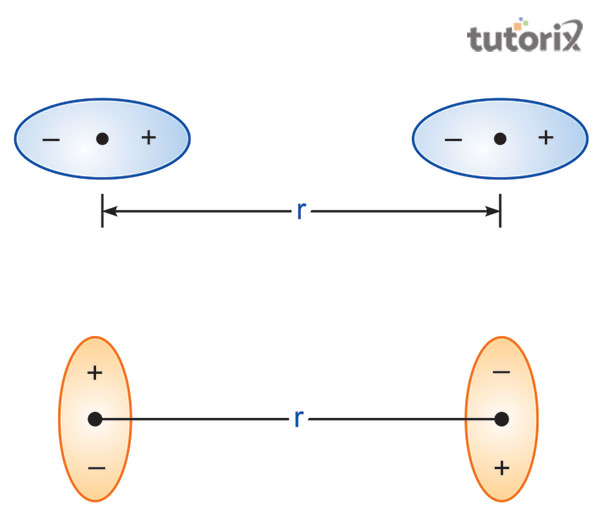
图3：范德华气体方程的相互作用

在范德华气体方程在可压缩流体上的应用中，流体成分的概念应该清晰。聚合物是一种可压缩流体，具有特定的体积，并且该体积通常用公式(p + A)(V - B) = CT表示，其中V表示特定体积，P表示压力，T表示温度，A、B、C是参数。

范德华方程的优缺点

优点

• 与理想气体相比，它可以更好地预测真实气体的实际行为，并且更准确。

• 此方程非常适用于流体气体对比（Kontogeorgis、Privat & Jaubert，2019）。

• 三次方程提供了三种不同类型的体积，这些体积适用于测量气体临界温度以上和以下的体积。

缺点

• 该方程仅获得临界温度以上的真实气体的真实数量

• 临界温度以下获得的温度也被接受。

• 就不同气体的过渡阶段而言，此方程失败了。

结论

该方程主要源自理想气体方程，该方程指出气体分子中存在一些点质量，这些点质量通过气体进行弹性碰撞。范德华方程被多次使用，因为气体方程无法正确解释真实气体的行为，并且为了推导出气体的物理状态，使用了该方程。

常见问题

问1 在范德华方程中，A和B常数指的是什么？

答：在范德华方程中，A和B常数指的是分子间力的修正。一摩尔中A和B常数的值指的是分子的原子。

问2 什么是理想气体定律？

答：理想气体定律陈述了假设理想气体状态下气体的通用方程。它主要用于评估气体在各种温度和条件下的行为。

问3 真实气体何时表现出其理想气体行为？

答：真实气体在较低温度下表现出理想气体的行为。在较高温度下，真实气体也表现出理想气体的行为。

问4 范德华方程的应用是什么？

答：根据理想气体定律，通过使用校正，可以很容易地推导出一个新方程，该方程利用该定律准确地确定真实气体的行为。此方程也适用于计算非理想条件下的气体性质。