火车运动机理及牵引力的推导

火车运动机理

下图显示了电力机车的基本机理。

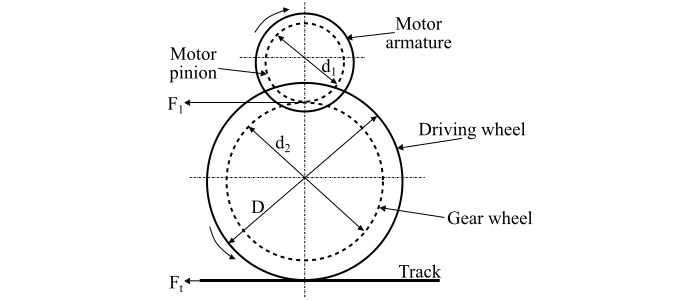
此处，驱动电机的电枢连接着一个直径为 d1 的小齿轮。小齿轮边缘的牵引力通过齿轮传动到驱动轮。

令：

• T = 电机输出扭矩，单位为 N_m

• F₁ = 小齿轮上的牵引力

• F_t = 车轮上的牵引力

• $\gamma$ = 齿轮传动比

• d₁ = 小齿轮直径

• d₂ = 齿轮直径

• D = 驱动轮直径

• $\eta$ = 电机到驱动轴的动力传递效率

因此，电机输出的扭矩由下式给出：

$$\mathrm{\mathit{T}\:=\:\mathit{F_{\mathrm{1}}}\:\times \:\frac{\mathit{d_{\mathrm{1}}}}{2}}$$

$$\mathrm{\therefore \mathrm{小齿轮上的牵引力,}\mathit{F_{\mathrm{1}}}\:=\:\frac{\mathrm{2}\mathit{T}}{\mathit{d_{\mathrm{1}}}}\:\:\:\cdot \cdot \cdot \mathrm{\left ( \mathrm{1} \right )}}$$

现在，传递到驱动轮的牵引力为：

$$\mathrm{\mathit{F_{\mathit{t}}}\:=\:\eta \mathit{F_{\mathrm{1}}}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{D}} \right )}\:=\:\eta \cdot \frac{\mathrm{2}\mathit{T}}{\mathit{d_{\mathrm{1}}}}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{D}} \right )}}$$

$$\mathrm{\Rightarrow \mathit{F_{\mathit{t}}}\:=\:\eta \mathit{T}\mathrm{\left ( \frac{\mathrm{2}}{\mathit{D}} \right )}\mathrm{\left ( \frac{\mathit{d_{\mathrm{2}}}}{\mathit{d_{\mathrm{1}}}} \right )}}$$

$$\mathrm{\because \mathrm{齿轮传动比,}\gamma\:=\: \:\frac{\mathit{d_{\mathrm{2}}}}{\mathit{d_{\mathrm{1}}}}}$$

$$\mathrm{\mathit{F_{\mathit{t}}}\:=\:\mathrm{2}\eta \gamma \mathrm{\left ( \frac{\mathit{T}}{\mathit{D}} \right )}\:\:\:\cdot \cdot \cdot \mathrm{\left ( \mathrm{2} \right )}}$$

公式 (2) 给出了驱动轮上牵引力的值。

驱动轮与轨道之间的最大摩擦力等于 $\mu$W。其中，μ 是驱动轮与轨道之间的粘着系数，W 是作用在驱动轴上的火车重量，称为粘着重量。粘着重量定义为作用在驱动轮上的总重量。

除非满足以下条件，否则不会发生打滑

$$\mathrm{\mathit{F_{t}}> \mu \mathrm{W}}$$

因此，为了使火车不打滑地运动，牵引力应小于或最多等于 $\mu$W。

从以上讨论可以清楚地看出，用于火车推进的牵引力的量值取决于作用在驱动轮上的重量以及驱动轮与轨道之间的粘着系数。

粘着系数

粘着系数定义为车轮不打滑时可施加的最大牵引力与粘着重量的比率，即：

$$\mathrm{\mu \:=\:\frac{\mathrm{车轮不打滑时可施加的最大牵引力}}{\mathrm{粘着重量}}}$$

此外，粘着系数会随着速度的增加而降低。干净干燥的铁轨的粘着系数的正常值为 0.25，而潮湿或油腻的铁轨的粘着系数低至 0.08。

由于在电力牵引中可以使用更高的牵引力值，因此可以使电力火车以更快的速度加速。这节省了时间，尤其是在停车距离较短的情况下。

数值示例

一列电力火车有 8 个电机与驱动轮相连，每个轮子的直径为 80 厘米。确定每个电机产生的扭矩以加速火车。使火车在 30 秒内加速到 50 公里/小时的速度所需的牵引力为 117590 牛顿，齿轮传动比为 4:1，齿轮传动效率为 85%。

解答

已知数据：

• 车轮直径，D = 80 厘米 = 0.8 米

• 牵引力，F_t = 117590 牛顿

• 齿轮传动比，$\gamma$ = 4

• 齿轮传动效率， $\eta$ = 85% = 0.85

因此，8 个电机产生的总扭矩为：

$$\mathrm{\mathit{T}\:=\:\frac{\mathit{F_{t}\times \mathit{D}}}{2\gamma \eta }\:=\:\frac{117590\times 0.8}{2\times 4\times 0.85}\:=\:13834.117\:\mathrm{NM}}$$

因此，每个电机产生的扭矩为：

$$\mathrm{\mathit{T_{\mathrm{each\:motor}}}\:=\:\frac{13834.117}{8}\:=\:1729.26\:\mathrm{NM}}$$

Manish Kumar Saini

更新于： 2022年5月3日

6K+ 次浏览

开启你的 职业生涯

通过完成课程获得认证

开始学习