列车牵引力

---

什么是牵引力？

推动机车车轮使列车前进所需的有效力称为**牵引力**。它用𝐹_𝑡表示，单位为牛顿。它是一个矢量，始终作用于机车车轮的切线方向。

列车牵引力

推动列车在轨道上行驶所需的总牵引力等于以下各项之和：

• 用于直线和角加速度的牵引力 (𝐹_𝑎)。

• 克服重力影响的牵引力 (𝐹_𝑔)。

• 克服列车阻力的牵引力 (𝐹_𝑟)。

因此，总牵引力表示为：

$$\mathrm{\mathit{F_{t}\mathrm{\: =\: }F_{a}\pm F_{g}\pm F_{r}}\; \cdot \cdot \cdot \left ( 1 \right )}$$

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

直线和角加速度的牵引力

根据动力学定律，使物体加速运动所需的力由下式给出：

$$\mathrm{力,\mathit{F}\mathrm{\: =\: }质量(\mathit{m})\times 加速度(\alpha )}$$

现在，考虑一辆重W吨的列车以α kmphps的加速度加速，则：

$$\mathrm{列车质量\mathrm{\: =\: }1000\mathit{W}\: kg}$$

$$\mathrm{加速度,\alpha \mathrm{\: =\: }\alpha \:kmphps\mathrm{\: =\: }\alpha \times \frac{1000}{3600}m/s^{2}\mathrm{\: =\: }0.2778\alpha \: m/s^{2} }$$

因此，直线加速度所需的牵引力为：

$$\mathrm{\mathit{F_{a}\mathrm{\: =\: }m\alpha \mathrm{\: =\: }\mathrm{1000}W\times \mathrm{0.2778\alpha } \mathrm{\: =\: }\mathrm{277.8}W\alpha}\: 牛顿$$

随着列车的直线加速，列车的旋转部件（如车轮和电机轴）也会在角方向加速。因此，所需的牵引力等于直线加速度所需的牵引力和旋转部件角加速度所需的牵引力的算术和。

实际上，角加速度所需的牵引力取决于需要角加速度的旋转部件的各个重量、回转半径等。因此，列车的等效加速重量取为𝑊_𝑒，其比W高8%到15%。

因此，直线和角加速度所需的牵引力由下式给出：

$$\mathrm{\mathit{F_{a}\mathrm{\: =\: }}277.8\, \mathit{W_{e}\alpha}\: 牛顿\; \; \cdot \cdot \cdot \left ( 2 \right )}$$

克服重力影响的牵引力

当列车处于坡度（或斜坡）上时，等于沿斜坡的死重分量的重力作用于列车，并趋于使其向下运动。因此，由于坡度产生的力由下式给出：

$$\mathrm{\mathit{F_{g}\mathrm{\: =\: }mg}\: sin\, \theta \mathrm{\: =\: } 1000 \mathit{W_{g}}\: sin\theta}$$

但是，在铁路工程中，坡度表示为在100米轨道距离内的高度上升（米），并表示为百分比坡度（G%）。现在从图中，我们有：

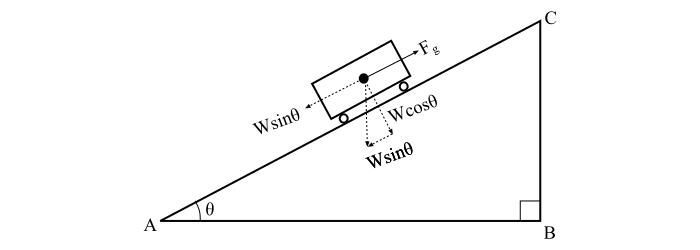
$$\mathrm{坡度或坡度,G \mathrm{\: =\: } sin\, \theta \mathrm{\: =\: }\frac{高度 \, (BC)}{沿轨道距离\: (AC)}}$$

$$\mathrm{\%G \mathrm{\: =\: } sin\, \theta \times 100}$$

$$\mathrm{\Rightarrow sin\, \theta \mathrm{\: =\: }\frac{\mathit{G}}{100}}$$

因此，

$$\mathrm{\mathit{F_{g}\mathrm{\: =\: }\mathrm{1000}Wg\times \frac{\mathit{G}}{\mathrm{100}}}\mathrm{\: =\: }10\mathit{WG}\times 9.81}$$

$$\mathrm{\Rightarrow \mathit{F_{g}\mathrm{\: =\: } \mathrm{9.81}\mathit{WG}}\; 牛顿\; \; \cdot \cdot \cdot \left ( 3 \right )}$$

其中，g = 9.81 m/s²，重力加速度。

克服列车阻力所需的牵引力

列车阻力包括当列车在直线平坦轨道上以均匀速度运行时抵抗列车运动的所有力。在这些条件下，驱动轴的全部能量输出都用于克服列车阻力。

列车阻力主要是由于：

• 滚动设备各个部件的摩擦。

• 轨道的摩擦。

• 空气阻力。

这里，前两个组成部分构成了列车阻力的机械阻力分量。此外，列车阻力还取决于轨道形状、尺寸和状况等各种因素，并以**每吨死重的牛顿**表示。对于普通列车，比阻值从40到70 N/吨不等。

因此，列车阻力的通用表达式为：

$$\mathit{R\mathrm{\: =\: }k_{\mathrm{1}}\mathrm{\: +\: }k_{\mathrm{2}}V\mathrm{\: +\: }k_{\mathrm{3}}V^{\mathrm{2}}}$$

其中，𝑘₁、𝑘₂和𝑘₃是常数，其值取决于列车和轨道。R是牛顿单位的阻力，V是kmph单位的速度。

因此，克服列车阻力所需的牵引力为

$$\mathit{F_{r}\mathrm{\: =\: }W\times r\; \; \cdot \cdot \cdot \mathrm{\left ( 4 \right )}}$$

其中，𝒓是列车死重每吨的比阻力。

因此，将方程式（2）、（3）和（4）中的值代入方程式（1），我们得到**运行列车所需的总牵引力**为：

$$\mathrm{\mathit{F_{t}\mathrm{\: =\: }F_{a}\pm F_{r}\mathrm{\: =\: }\mathrm{277.8}W_{e}\alpha \pm \mathrm{98.1}WG\mathrm{\: +\: }Wr}\: \: \cdot \cdot \cdot \left ( 5 \right )}$$

这里，+号表示向上坡运动，-号表示向下坡运动。