电动列车比能量输出的确定

能量输出是指列车推进所需的能量，主要用于将列车从静止加速到最大速度 (V_m)，以及克服坡度和轨道运行阻力所需的能量。

比能量输出定义为：

$$\mathrm{比能量输出\: =\: }\frac{以瓦时计的能量输出}{以吨计的列车重量\times以公里计的运行距离}$$

比能量输出的单位为瓦时/吨公里。比能量输出用于比较不同时刻运行的列车的动态性能。

电动列车比能量输出的确定

假设列车按照图中所示的简化梯形速度-时间曲线运行。

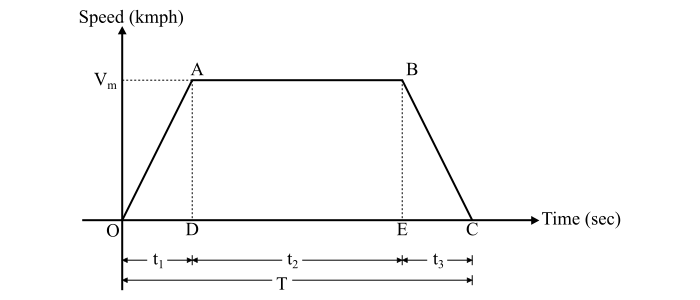
考虑一条在整个运行过程中坡度为 G% 的轨道。则：

将列车从静止加速到速度 𝑽_𝒎 的能量输出（设为 𝐸₁）−

$$\mathrm{\mathit{E_{\mathrm{1}}}\mathrm{\: =\: }\frac{1}{2}\frac{\mathit{F_{t}V_{m}}}{3600}\times \frac{\mathit{t_{\mathrm{1}}}}{3600}\: kWh}$$

其中，𝐹_𝑡 为牵引力。

$$\mathrm{\mathit{\Rightarrow E_{\mathrm{1}}}\mathrm{\: =\: }\frac{1}{2}\frac{\mathit{F_{t}V_{m}}}{3600}\times \frac{\mathit{V_{m}}}{3600\alpha }\: kWh}\; \; \left ( \because \mathit{t_{\mathrm{1}}\mathrm{\: =\: }\frac{V_{m}}{\alpha }} \right )$$

$$\mathrm{\mathit{\because F_{t}}\mathrm{\: =\: }277.8\mathit{W_{e}\alpha \mathrm{\: +\: }\mathrm{98.1}WG\mathrm{\: +\: }W.r}}$$

$$\mathit{\therefore E_{\mathrm{1}}\mathrm{\: =\: }\mathrm{\frac{1}{2}}\times \frac{V_{m}^{\mathrm{2}}}{\mathrm{\left ( 3600 \right )^{2}}\alpha }\left [ \mathrm{277.8}W_{e}\alpha \mathrm{\: +\: }\mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\; \; \mathrm{kWh …(1)}}$$

以速度 𝑽_𝒎 抵抗坡度和运行阻力的能量输出（设为 𝐸₂）−

$$\mathrm{\mathit{E_{\mathrm{2}}\mathrm{\: =\: }\frac{F_{t}^{'}V_{m}}{\mathrm{3600}}\times \frac{t_{\mathrm{2}}}{\mathrm{3600}}}\; kWh}$$

$$\mathrm{\because 自由运行期间行驶的距离,\mathit{S^{'}\mathrm{\: =\: }\frac{V_{m}t_{\mathrm{2}}}{\mathrm{3600}}}}$$

$$\mathrm{\therefore \mathit{E_{\mathrm{2}}\mathrm{\: =\: }\frac{F_{t}^{'}\times S'}{\mathrm{3600}}}\;kWh }$$

$$\mathrm{\Rightarrow \mathit{E_{\mathrm{2}}\mathrm{\: =\: }\left [ \mathrm{98.1\, WG\mathrm{\: +\: }W\cdot r} \right ]\times \frac{s'}{\mathrm{3600}}}\; kWh\; \; \cdot \cdot \cdot \left ( 2 \right )}$$

因此，整个运行的总能量输出由下式给出：

$$\mathit{ E\mathrm{\: =\: }\left\{\mathrm{\frac{1}{2}}\times \frac{V_{m}^{\mathrm{2}}}{\mathrm{\left ( 3600 \right )^{2}}\alpha }\left [ \mathrm{277.8}W_{e}\alpha \mathrm{\: +\: }\mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\times \frac{s'}{\mathrm{3600}}\; \right\}\mathrm{kWh}}$$

$$\mathit{\Rightarrow E\mathrm{\: =\: }\left\{ \frac{V_{m}^{\mathrm{2}}\times \mathrm{1000}}{\mathrm{\mathrm{2}\alpha\left ( 3600 \right )^{2}} }\left [ \mathrm{277.8}W_{e}\alpha \mathrm{\: +\: }\mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\times \frac{s'\times \mathrm{1000}}{\mathrm{3600}}\; \mathrm{Wh} \right\}}$$

$$\mathit{\Rightarrow E\mathrm{\: =\: }\frac{V_{m}^{\mathrm{2}}}{\mathrm{2}\alpha}\times \frac{\mathrm{1000}}{\mathrm{\left ( 3600 \right )^{2}} }\times \mathrm{277.8}W_{e}\alpha \mathrm{\: +\: }\frac{V_{m}^{\mathrm{2}}}{\mathrm{2}\alpha}\times \frac{\mathrm{1000}}{\mathrm{\left ( 3600 \right )^{2}} } \left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r \right ]\times \frac{s'\times \mathrm{1000}}{\mathrm{3600}} }$$

$$\mathrm{\Rightarrow \mathit{E\mathrm{\: =\: }\mathrm{0.01072}V_{m}^{\mathrm{2}}W_{e}\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r\right ] \left [ \frac{V_{m}^{\mathrm{2}}}{\mathrm{2 \alpha \times 3600}}\mathrm{\: +\: }S^{'} \right ]\times \mathrm{\frac{1000}{3600}}}}$$

$$\mathrm{\Rightarrow \mathit{E\mathrm{\: =\: }\mathrm{0.01072}V_{m}^{\mathrm{2}}W_{e}\mathrm{\: +\: }\left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r\right ] \left [ S^{"}\mathrm{\: +\: }S^{'} \right ]\times \mathrm{\frac{1000}{3600}}}}$$

其中，𝑆" 为加速期间行驶的距离。

现在，如果 𝑆₁ = 𝑆" + 𝑆′ 是加速和自由运行期间行驶的距离（以公里计）。那么，我们有：

$$\mathrm{\Rightarrow \mathit{E\mathrm{\: =\: }\mathrm{0.01072}V_{m}^{\mathrm{2}}W_{e}\mathrm{\: +\: }\mathrm{0.2778} \left [ \mathrm{98.1}WG\mathrm{\: +\: }W\cdot r\right ] S_{\mathrm{1}}}\: \: \cdot \cdot \cdot \left ( 3 \right )}$$

因此，根据比能量输出的定义，我们得到：

$$\mathrm{比能量输出=\frac{0.01072\, \mathit{V{_{m}}^{\mathrm{2}}W_{e}}+0.2778\left [ 98.1\mathit{WG+W \cdot r} \right ]\times \mathit{S}_{1}}{\mathit{W\times S}}}$$

$$\mathrm{比能量输出 \mathrm{\: =\: } \mathit{\frac{\mathrm{0.01072}V_{m}^{\mathrm{2}}}{S}\times \frac{W_{e}}{W}\mathrm{\: +\: }\mathrm{0.2778}\frac{S_{\mathrm{1}}}{S}\left ( \mathrm{98.1}G\mathrm{\: +\: }r \right )\; \; \cdot \cdot \cdot }\left ( 4 \right )}$$

如果轨道是平的，即 G = 0，则比能量输出为：

$$\mathrm{比能量输出 \mathrm{\: =\: } \mathit{\frac{\mathrm{0.01072}V_{m}^{\mathrm{2}}}{S}\times \frac{W_{e}}{W}\mathrm{\: +\: }\mathrm{0.2778}\, \frac{S_{\mathrm{1}}}{S}\, r\; \; \cdot \cdot \cdot }\left ( 5 \right )}$$

Saini Manish Kumar

更新于：2022年5月23日

2K+ 次浏览

开启您的职业生涯

完成课程获得认证

开始学习