玻尔半径 - 定义和推导

---

引言

玻尔原子模型是原子结构研究领域的一项重大突破。原子是所有物质的基本单位。根据玻尔原子模型，原子包含一个小的中心核心，称为原子核，充满了正电荷。电子围绕原子核在称为轨道的特定圆圈中运行。

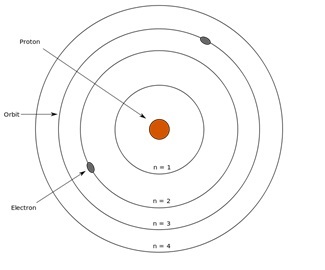
Sharon Bewick, 玻尔模型, CC BY-SA 3.0

圆形路径由电子和原子核之间静电力产生的向心力维持。

原子模型

为了解释原子的结构，人们开发了多种模型。这些模型是由约翰·道尔顿、J.J.汤姆逊、欧内斯特·卢瑟福、尼尔斯·玻尔和埃尔温·薛定谔提出的。

道尔顿原子模型

根据道尔顿的理论，所有物质都由称为原子的微小粒子组成。元素中的所有原子看起来都一样。不同元素的原子具有不同的性质。但他未能解释原子的结构。

汤姆逊原子模型

J.J.汤姆逊是第一个解释原子精细结构的人。他提出原子是像云一样散布的带正电的粒子。根据这种说法，带负电的电子散布在一个带正电的云中，看起来像西瓜或布丁里的李子。这就是为什么它被称为**李子布丁模型**。由于无法得到实验支持，该模型也失败了。

卢瑟福原子模型

欧内斯特·卢瑟福进行了**α散射**实验来提出他的原子模型。他注意到大多数α粒子穿过了金箔。少数粒子发生轻微偏转。极少数粒子沿相同路径反弹。因此，他通过实验提出，中心存在一个带正电的原子核。它的质量远小于原子。电子围绕原子核作圆周运动。但它**无法**解释**原子的稳定性**。

玻尔原子模型

尼尔斯·玻尔克服了卢瑟福原子模型的缺点。根据他的实验结果，他得出结论：原子包含一个带正电粒子的原子核。由于电子和质子之间的吸引力，电子在圆形轨道上围绕原子核旋转。它在具有特定能量的特定轨道上旋转。在旋转过程中，它不会损失或获得能量。但当电子从一个轨道跃迁到另一个轨道时，它会发射能量。他利用了量子化的概念。要充分了解**玻尔半径**，有必要了解玻尔原子模型和普朗克量子理论。

普朗克量子理论

该理论解释了辐射的发射和吸收以及电子的波动性。根据该理论，当电子在能级之间跃迁时，它会以能量量子（称为光子）的形式发射能量。这种能量与辐射频率成正比。

$$\mathrm{E\:\propto\:v}$$

$$\mathrm{E = hv}$$

h=普朗克常数 $\mathrm{=6.626×10^{−34}\:J. sec}$

玻尔原子模型的假设

玻尔的假设基于普朗克量子理论。根据该理论，电子围绕原子核在具有确定能量的确定轨道上旋转，并且具有确定的量子数。当电子在轨道之间跃迁时，它们会发射能量量子，这由普朗克方程给出。由于电子在具有固定角动量的轨道上运动，因此角动量是量子化的。

$$\mathrm{mvr =\frac{nh}{2\pi}\:\:\:\:\:n = 1, 2, 3, ……}$$

什么是玻尔半径？

根据玻尔的理论，原子的半径是原子核和原子最外层电子壳层之间的距离。准确地说，它是氢原子基态下原子核和电子之间的距离。尼尔斯·玻尔推导出的玻尔半径公式为

$$\mathrm{a_0=(\frac{\epsilon_0 h^2}{\pi me^2})n^2}$$

玻尔半径公式

让我们考虑一个质量为m、电荷为e的电子围绕有效电荷为$\mathrm{Ze^+}$的原子核运动。假设电子以速度v在半径为$\mathrm{a_0}$的轨道上围绕原子核运动。根据库仑定律，带电粒子之间存在吸引力，其表达式为

$$\mathrm{F=\frac{q_1 q_2}{4\pi\epsilon_0 a_0^2}}$$

现在应用于静电力：

$$\mathrm{F =\frac{Ze^2}{4\pi\epsilon_0 a_0^2}\:\:\:\:\:………. (1)}$$

电子由于向心力$\mathrm{(F_c)}$而在圆形轨道上运动。

$$\mathrm{F_c =\frac{mv^2}{a_0}………. (2)}$$

比较方程（1）和（2），我们得到：

$$\mathrm{\frac{mv^2}{a_0}=\frac{Ze^2}{4\pi\epsilon_0 a_0^2}}$$

$$\mathrm{mv^2=\frac{Ze^2 \:a_0}{4\pi\epsilon_0 a_0^2}}$$

$$\mathrm{mv^2=\frac{Ze^2}{4\pi\epsilon_0 a_0}\:\:\:………. (3)}$$

由此我们得到：

$$\mathrm{a_0=\frac{Ze^2}{4\pi\epsilon_0 mv^2}}$$

这个方程表明电子的半径与速度成反比，这意味着快速运动的电子在较低的轨道上。根据玻尔的假设，角动量由下式给出：

$$\mathrm{mva_0=\frac{nh}{2\pi}}$$

$$\mathrm{v=\frac{nh}{2\pi ma_0}}$$

将该方程平方：

$$\mathrm{v^2=\frac{n^2 h^2}{4\pi^2 m^2 a_0^2}\:\:\:…………. (5)}$$

将方程（5）代入方程（4），我们得到：

$$\mathrm{a_0=\frac{Ze^2}{4\pi\epsilon_0 m(\frac{n^2 h^2}{4\pi^2 m^2 a_0^2})}}$$

$$\mathrm{a_0=\frac{Ze^24\pi^2 m^2 a_0^2}{4\pi\epsilon_0 mn^2 h^2}}$$

$$\mathrm{a_0=\frac{Ze^2 \pi ma_0^2}{\epsilon_0 n^2 h^2}}$$

$$\mathrm{a_0=\frac{\epsilon_0 n^2 h^2}{Ze^2 \pi m}}$$

对于氢原子，Z=1。因此

$$\mathrm{a_0=\frac{\epsilon_0 n^2 h^2}{e^2 \pi m}}$$

$$\mathrm{a_0=(\frac{\epsilon_0 h^2}{e^2 \pi m})n^2}$$

这里$\mathrm{\frac{\epsilon_0 h^2}{e^2 \pi m}}$是一个常数。

因此，玻尔半径与轨道数的平方成正比。通过代入常数项的值

$$\mathrm{\frac{\epsilon_0 h^2}{e^2 \pi m}= 0.529\:Å}$$

因此

$$\mathrm{a_0=0.529Å\:n^2}$$

玻尔半径的应用和用途

虽然它有一些应用，例如玻尔半径用于计算一些物理量，如原子单位和精细结构常数等。

结论

原子是物质的基本单位。原子的结构在许多时期都被许多科学家提出。本文讨论了尼尔斯·玻尔提出的模型，并在此讨论了玻尔半径。本文详细推导了玻尔半径的公式。

常见问题

Q1. 静电吸引是什么意思？

A1. 它是原子带电粒子之间发生的无接触的吸引或排斥力。

Q2. 卢瑟福是如何进行散射实验的？

A2. 将金金属拉成厚度为100nm的薄箔，并用α粒子轰击。散射的α粒子收集在圆形屏幕上。

Q3. 玻尔原子模型的局限性是什么？

A3. 玻尔原子模型无法解释塞曼效应和斯塔克效应，也无法解释海森堡测不准原理。这些都是玻尔原子模型的局限性。

Q4. 什么是海森堡测不准原理？

A4. 海森堡测不准原理描述的是不可能同时找到电子的位置和动量。

Q5. 玻尔半径与量子数之间有什么关系？

A5. 玻尔半径与量子数成正比。随着量子数的增加，玻尔半径也增加。