数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学什么是语法树（推导树）？
推导是指用产生式右边的式子替换给定字符串的非终结符。从开始符号生成完整的终结符字符串的规则应用序列称为推导。语法树是推导的图形表示。因此，它也称为推导树。推导树独立于产生式使用的顺序。
语法树是一个有序树，其中节点用产生式的左边标记，节点的子节点定义其等效的右边。语法树也称为语法树、生成树或产生式树。
对于 CFG G =(V,∑, P,S)，语法树是一个满足以下条件的树：
根节点的标签为 S，其中 S 是开始符号。
语法树的每个顶点都有一个标签，可以是变量 (V)、终结符 (Σ) 或 ε。
如果 A → C1,C2…….Cn 是一个产生式，那么 C1,C2…….Cn 是标记为 A 的节点的子节点。
叶子节点是终结符 (Σ)，内部节点是变量 (V)。
内部顶点的标签始终是变量。
如果顶点 A 有 k 个子节点，其标签为 A1,A2…….Ak，则 A →
A1,A2…….Ak 将是上下文无关文法 G 中的产生式。
产出 (Yield) − 推导树的产出是从左到右对叶子节点标签的串联。
示例 1 − 如果 CFG 有产生式。
S → a A S | a S → Sb A | SS | ba
证明 S ⇒ *aa bb aa 并构造产出为 aa bb aa 的语法树。
解答
S ⇒lm lm a $\underline{A}$ S
⇒ a $\underline{S\:b}$ A S
⇒ aa b $\underline{A}$ S
⇒ aa bba $\underline{S}$
∴ S ⇒ * aa bb aa
推导树
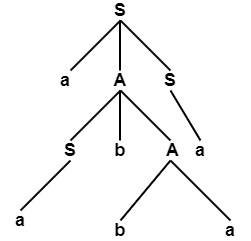
产出 = 叶子节点从左到右的顺序 = aa bb aa
示例 2
考虑 CFG
S → bB | aA A → b | bS | aAA B → a |aS | bBB
找到 (a) 最左
字符串 b aa baba 的最右推导。也找到推导树。
解答
- 最左推导
S⇒b $\underline{B}$
⇒ bb $\underline{B}$B
⇒ bba$\underline{B}$
⇒ bbaa$\underline{S}$
⇒ bb aa$\underline{bB}$
⇒ bb aa b $\underline{aS}$
⇒ bb aa bab $\underline{B}$
⇒ bb aa ba ba
- 最右推导
S ⇒ b$\underline{B}$
⇒ bb B$\underline{B}$
⇒ bbBa$\underline{S}$
⇒ bbBab$\underline{B}$
⇒ bbBaba$\underline{S}$
⇒ bbBabab$\underline{B}$
⇒ bb$\underline{B}$abab a
⇒ bbaababa
示例 3 − 考虑以下给出的语法：
E⇒ E+E|E $\ast$ E|id
查找
- 最左
- 字符串的最右推导。
解答
- 最左推导
E ⇒ $\underline{E}$+E
⇒ $\underline{E}$+E+E
⇒ id+E+E
⇒ id+id+E
⇒ id+id+id
- 最右推导
E ⇒ E+$\underline{E}$
⇒ E+E+$\underline{E}$
⇒ E+E+id
⇒ E+id+id
⇒ id+id+id
13K+ 浏览量
