连通性、距离和生成树

生成树

一个简单的定义是，树是一个与之关联的无环连通图，其中一个环允许我们从一个节点返回到自身而不重复任何边。

连通图 G 的生成树定义为包含 G 所有顶点的树。

生成树常用于互联网路由算法。在互联网中，计算机（节点）通常通过许多冗余的物理连接连接。

图中生成树的总数。如果一个图是一个具有 n 个顶点的完全图，则生成树的总数为 n^(n-2)

其中 n 表示图中节点的数量。在完全图中，该任务等价于计算具有 n 个节点的不同标记树，这可以使用凯莱公式。

连通性

在数学和计算机科学中，连通性是图论的基本概念之一

它需要移除的最少元素（节点或边）数量，以将剩余节点分离成孤立的子图。

它与网络流问题的理论密切相关。

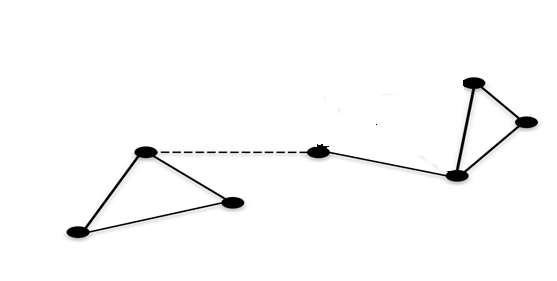
当虚线边被移除时，此图变得不连通。

顶点连通性。图的顶点连通性是删除其会导致图断开连接的最少节点数。

顶点连通性有时表示为“点连通性”或简称为“连通性”。

边连通性。从图中删除其会导致图断开连接的最少边数，也称为线连通性。

不连通图的边连通性为 0，而与图桥关联的连通图的边连通性为 1。

距离

两个节点之间的距离可以用最低公共祖先来计算。以下是公式。

Dist(d1, d2) = Dist(root, d1) + Dist(root, d2) - 2*Dist(root, lca)
'd1' and 'd2' are the two given keys
'root' is root of given Binary Tree.
'lca' is lowest common ancestor of d1 and d2
Dist(d1, d2) is the distance between d1 and d2.

更新于： 2020年1月2日

487 次查看

开启你的 职业生涯

通过完成课程获得认证

开始学习
广告