使用 Python Networkx 的聚类、连通性和其他图属性

---

Python NetworkX 是一个流行的开源 Python 库，用于创建、操作和分析复杂的网络或图。它提供了广泛的工具、算法和函数来处理图，使其成为网络分析和研究的宝贵资源。

Python NetworkX 允许我们表示和处理不同类型的图，例如有向图、无向图、多重图（节点之间有多条边的图）和加权图（具有边权重的图）。它还提供了一个简单直观的接口来创建、添加节点和边，以及对图执行各种操作。

NetworkX 的安装和导入

要使用 NetworkX，我们必须使用 Python 包管理器 pip 安装它，在命令提示符中运行以下命令。

pip install networkx

一旦 NetworkX 安装在我们的 Python 环境中，我们就可以在 Python 脚本或交互式环境中导入该库，并通过执行以下命令开始使用其功能。

import networkx as nx

NetworkX 库提供了广泛的属性，例如聚类、连通性和其他图属性，让我们在本文中详细了解它们。

聚类系数

聚类系数是衡量图中节点聚集在一起程度的指标。它量化了图中三角形的数量，其中三角形由三个相互连接的节点组成。较高的聚类系数表示图中的节点更有可能形成紧密连接的集群。

在 NetworkX 中，我们可以使用 average_clustering() 函数计算聚类系数以获得图的平均聚类系数，或者使用 clustering() 函数计算各个节点的聚类系数。

平均聚类系数

NetworkX 中的 average_clustering() 函数计算图的平均聚类系数。它返回一个表示图中所有节点的平均聚类系数的单个值。计算平均聚类系数的公式基于每个节点的局部聚类系数和节点数。

示例

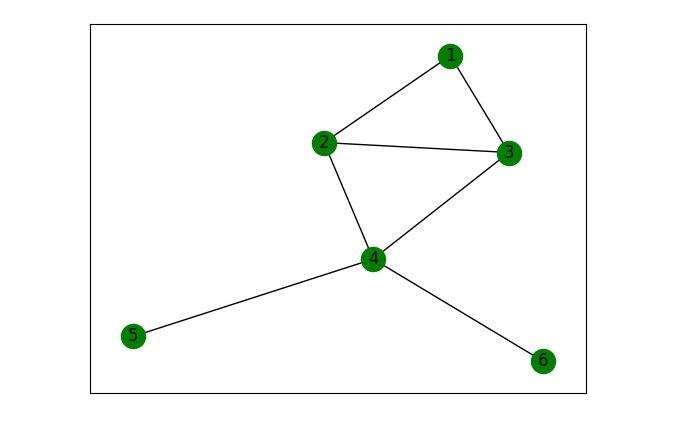
在此示例中，我们使用 nx.Graph() 函数创建一个简单的无向图，并使用 add_edges_from() 函数添加边。然后，我们使用 nx.average_clustering() 计算平均聚类系数，并打印结果以及使用 nx.draw_network() 函数绘制图形。

import networkx as nx
import matplotlib.pyplot as plt

G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (4, 5), (4, 6)])
avg_clustering = nx.average_clustering(G)
nx.draw_networkx(G, with_labels = True, node_color ='green')
print("Average Clustering Coefficient:", avg_clustering)

输出

Average Clustering Coefficient: 0.4166666666666666

节点聚类系数

NetworkX 中的 clustering() 函数计算图中各个节点的聚类系数。它返回一个字典，其中键是图中的节点，值是它们相应的聚类系数。

节点的聚类系数计算为节点邻居之间连接数与可能连接总数的比率。

示例

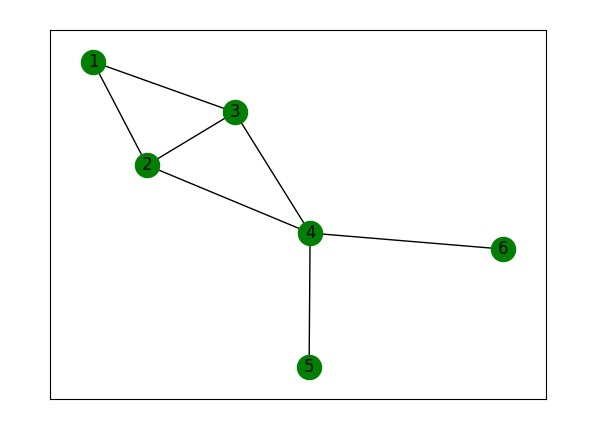
在此示例中，我们创建一个图并添加边。然后，我们使用 nx.clustering() 计算每个节点的聚类系数，并使用循环打印结果。

import networkx as nx
import matplotlib.pyplot as plt

# Create a graph
G = nx.Graph()
G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4), (3, 4), (4, 5), (4, 6)])
# Calculate the clustering coefficient of each node
node_clustering = nx.clustering(G)
print("Node Clustering Coefficients:")
for node, clustering_coefficient in node_clustering.items():
   print(f"Node {node}: {clustering_coefficient}")
nx.draw_networkx(G, with_labels = True, node_color ='green')

输出

Node Clustering Coefficients:
Node 1: 1.0
Node 2: 0.6666666666666666
Node 3: 0.6666666666666666
Node 4: 0.16666666666666666
Node 5: 0
Node 6: 0

连通性

连通性是指图的属性，该属性决定了所有节点是否都可以从任何其他节点到达。NetworkX 提供了确定图连通性的函数，例如 is_connected() 和 is_strongly_connected()。

示例

在此示例中，我们创建一个图并添加边。然后，我们使用 nx.is_connected() 检查图是否连接。如果所有节点都可以从任何其他节点到达，则该函数返回 True，否则返回 False。

import networkx as nx
import matplotlib.pyplot as plt

# Create a graph
G = nx.Graph()
G.add_edges_from([(1, 2), (2, 3)])
# Check if the graph is connected
connected = nx.is_connected(G)
print("Is Graph Connected?", connected)
nx.draw_networkx(G, with_labels = True, node_color ='green')

输出

Is Graph Connected? True

度中心性

度中心性是一种量化节点重要性或中心性的指标，基于其度，即连接数。NetworkX 提供了 degree_centrality() 函数来计算图中节点的度中心性。

示例

在此示例中，我们创建一个图并添加边。然后，我们使用 nx.degree_centrality() 计算度中心性并打印结果，该结果给出节点及其对应度中心性值的字典。

import networkx as nx
import matplotlib.pyplot as plt

# Create a graph
G = nx.Graph()
G.add_edges_from([(1, 2), (2, 3), (2, 4), (3, 4), (4, 5), (4, 6)])
# Calculate degree centrality
centrality = nx.degree_centrality(G)
print("Degree Centrality:", centrality)
nx.draw_networkx(G, with_labels = True, node_color ='blue')

输出

Degree Centrality: {1: 0.2, 2: 0.6000000000000001, 3: 0.4, 4: 0.8, 5: 0.2, 6: 0.2}