数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学图的连通性
能否从一个顶点遍历到图的另一个顶点取决于图的连接方式。连通性是图论中的一个基本概念。连通性定义了图是连通的还是不连通的。它根据边和顶点有子主题，称为边连通性和顶点连通性。让我们详细讨论它们。
连通性
如果**每对顶点之间都存在一条路径**，则称该图是**连通的**。从每个顶点到任何其他顶点，都应该存在一些路径可以遍历。这就是图的连通性。具有多个不连通顶点和边的图被称为不连通图。
示例1
在下面的图中，可以从一个顶点遍历到任何其他顶点。例如，可以使用路径“a-b-e”从顶点“a”遍历到顶点“e”。
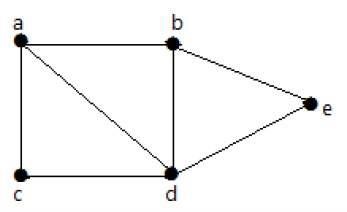
示例2
在下面的示例中，无法从顶点“a”遍历到顶点“f”，因为它们之间不存在直接或间接的路径。因此，它是一个不连通图。
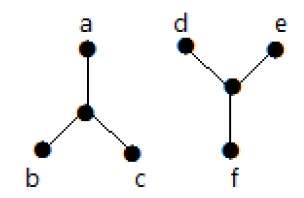
连通性类型
图的连通性大致可以分为两类：
边连通性
顶点连通性
边连通性
设“G”是一个连通图。移除使得“G”不连通的最小边数称为G的边连通性。
**符号** − λ(G)
换句话说，**G的最小割集中的边数**称为G的边连通性。
如果“G”有一条割边，则*λ(G)*为1。（G的边连通性。）
示例
看一下下面的图。通过移除两条最小边，连通图变得不连通。因此，它的边连通性(λ(G))为2。
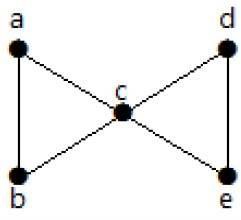
这里有四种通过移除两条边来断开图连接的方法：
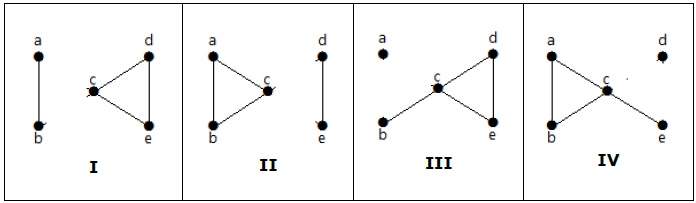
顶点连通性
设“G”是一个连通图。移除使得“G”变得不连通或将“G”简化为平凡图的最小顶点数称为它的顶点连通性。
**符号** − K(G)
示例
在上图中，移除顶点“e”和“i”会使图不连通。
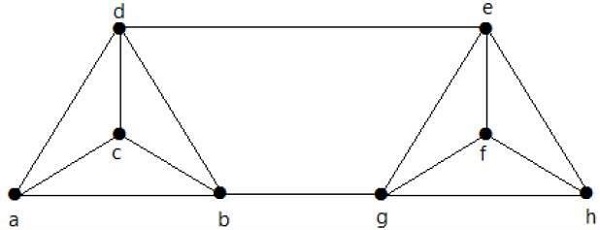
如果G有一个割顶，则K(G) = 1。
**符号** − 对于任何连通图G，
K(G) ≤ λ(G) ≤ δ(G)
顶点连通性 (K(G))，边连通性 (λ(G))，G 的最小度数 (δ(G))。
示例
计算以下图的λ(G)和K(G)：
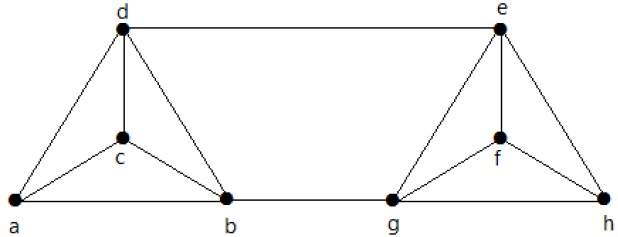
解答
从图中，
δ(G) = 3
K(G) ≤ λ(G) ≤ δ(G) = 3 (1)
K(G) ≥ 2 (2)
删除边 {d, e} 和 {b, h}，我们可以断开 G 的连接。
因此，
λ(G) = 2
2 ≤ λ(G) ≤ δ(G) = 2 (3)
从 (2) 和 (3) 可知，顶点连通性 K(G) = 2
423 次浏览
