数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究最小瓶颈生成树 (MBST)
最小瓶颈生成树是指一个无向图，其最大权重尽可能小。
让我们举个例子来理解最小瓶颈生成树。
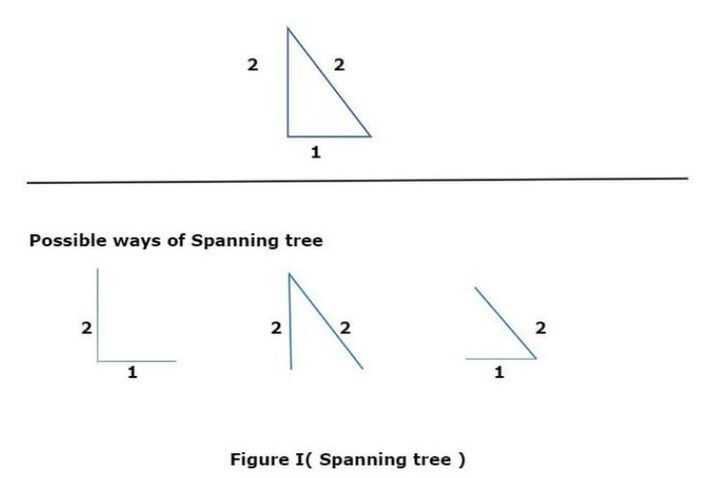
在图 I 中，我们观察到有三种可能的生成树具有公共边 2，这意味着没有其他树的瓶颈值小于 2。因此，所有这些树都验证为最小瓶颈生成树。
我们如何说最小生成树是 MBST？
以下几点可以帮助理解最小生成树成为 MBST 的条件：
MBST 从技术上讲不是最小生成树。
具有最大边权重的最大边是最小瓶颈生成树。
最小生成树必须是 MBST。
MBST 的总权重大于最小生成树。
在本文中，我们将深入了解最小瓶颈生成树。
示例 1
设 G 为给定的矩形图，并找到所有可能的生成树。
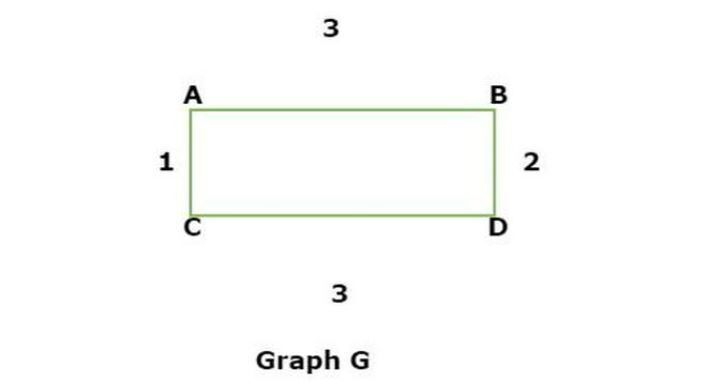
现在我们必须找到生成树的所有可能方式，例如：
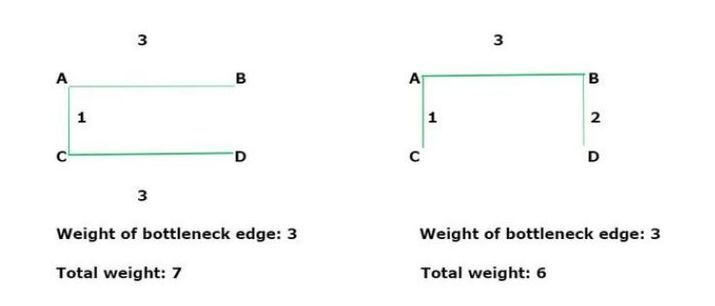
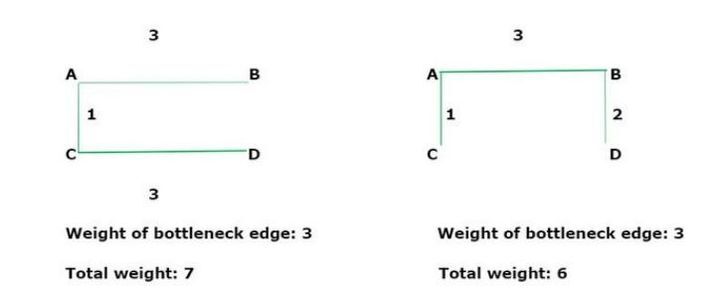
我们看到有 4 种可能的生成树，它们说明了给定无向图的不同形式。通过完成所有这些生成，有一个生成树的权重为 6。所有指定图的生成树都是最小瓶颈生成树，因为它们都具有相同的瓶颈边值。但是，只有两个生成树的总权重是最小的 (6)，其余的不是最小生成树。
MBST（最小瓶颈生成树）与 MST（最小生成树）有什么区别？
现在让我们看以下三张图片来理解 MST 和 MBST 之间的区别
以下几点可以帮助理解所有这些生成图：
给定的图 I 表示原始图，总权重 (10+40+30+50+30+20) 为 180。
为了找到图的 MST，我们将图分成两个图，即图 II 和图 III。
图 II 的最小权重 (10+30+30) 为 70。
图 III 的最小权重 (10+20+30) 为 60。
因此，图 III 的结果显示了可能的最佳最小生成树。
图 II 表示 MBST，而图 III 表示 MST。
因此，MST 必须是 MBST，而 MBST 并不总是被认为是 MST。
结论
我们探讨了最小瓶颈生成树的概念，它通过给出边的最大权重以不同的形式表示图。我们看到了两个例子，它们使 MST 与 MBST 的对比更加清晰。MBST 的实际应用包括电信、供应链系统、供水网络等。
513 次查看
