数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
安卓
Python
C编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
时装研究
法律克鲁斯卡尔（最小生成树）MST算法
G(V,E)是有连接的图，且给定了每条边的权重或代价。克鲁斯卡尔算法将使用此图和代价找出最小生成树。
该算法采用合并树的方法。最初，有多棵不同的树，此算法将通过选取代价最小的边将这些树合并，形成一棵独立的树。
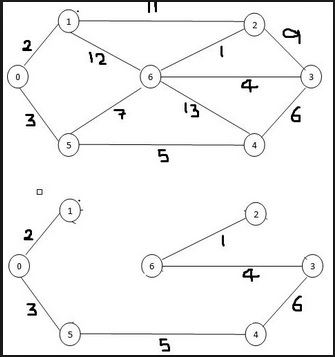
在这个问题中，列出所有边，并根据其代价进行排序。从列表中，选出代价最小的边添加到树中，并检查每条边是否形成了回路，如果形成了回路，则从列表中舍弃该边，然后查找下一条边。
此算法的时间复杂度为O(E log E)或O(E log V)，其中E是边的数量，V是顶点的数量。
输入 - 邻接矩阵
0 1 3 4 ∞ 5 ∞ 1 0 ∞ 7 2 ∞ ∞ 3 ∞ 0 ∞ 8 ∞ ∞ 4 7 ∞ 0 ∞ ∞ ∞ ∞ 2 8 ∞ 0 2 4 5 ∞ ∞ ∞ 2 0 3 ∞ ∞ ∞ ∞ 4 3 0
输出 -
Edge: B--A And Cost: 1 Edge: E--B And Cost: 2 Edge: F--E And Cost: 2 Edge: C--A And Cost: 3 Edge: G--F And Cost: 3 Edge: D--A And Cost: 4 Total Cost: 15
算法
kruskal(g: 图，t: 树)
输入 - 给定的图g和一棵空树t
输出 - 选定边的树t
Begin create set for each vertices in graph g for each set of vertex u do add u in the vertexSet[u] done sort the edge list. count := 0 while count <= V – 1 do //as tree must have V – 1 edges ed := edgeList[count] //take an edge from edge list if the starting vertex and ending vertex of ed are in same set then merge vertexSet[start] and vertexSet[end] add the ed into tree t count := count + 1 done End
示例
#include<iostream>
#define V 7
#define INF 999
using namespace std;
//Cost matrix of the graph
int costMat[V][V] = {
{0, 1, 3, 4, INF, 5, INF},
{1, 0, INF, 7, 2, INF, INF},
{3, INF, 0, INF, 8, INF, INF},
{4, 7, INF, 0, INF, INF, INF},
{INF, 2, 8, INF, 0, 2, 4},
{5, INF, INF, INF, 2, 0, 3},
{INF, INF, INF, INF, 4, 3, 0}
};
typedef struct{
int u, v, cost;
}edge;
void swapping(edge &e1, edge &e2){
edge temp;
temp = e1;
e1 = e2;
e2 = temp;
}
class Tree{
int n;
edge edges[V-1]; //as a tree has vertex-1 edges
public:
Tree(){
n = 0;
}
void addEdge(edge e){
edges[n] = e; //add edge e into the tree
n++;
}
void printEdges(){ //print edge, cost and total cost
int tCost = 0;
for(int i = 0; i<n; i++){
cout << "Edge: " << char(edges[i].u+'A') << "--" << char(edges[i].v+'A');
cout << " And Cost: " << edges[i].cost << endl;
tCost += edges[i].cost;
}
cout << "Total Cost: " << tCost << endl;
}
};
class VSet{
int n;
int set[V];//a set can hold maximum V vertices
public:
VSet(){
n = -1;
}
void addVertex(int vert){
set[++n] = vert; //add vertex to the set
}
int deleteVertex(){
return set[n--];
}
friend int findVertex(VSet *vertSetArr, int vert);
friend void merge(VSet &set1, VSet &set2);
};
void merge(VSet &set1, VSet &set2){
//merge two vertex sets together
while(set2.n >= 0)
set1.addVertex(set2.deleteVertex());
//addToSet(vSet1, delFromSet(vSet2));
}
int findVertex(VSet *vertSetArr, int vert){
//find the vertex in different vertex sets
for(int i = 0; i<V; i++)
for(int j = 0; j<=vertSetArr[i].n; j++)
if(vert == vertSetArr[i].set[j])
return i;//node found in i-th vertex set
}
int findEdge(edge *edgeList){
//find the edges from the cost matrix of Graph and store to edgeList
int count = -1, i, j;
for(i = 0; i<V; i++)
for(j = 0; j<i; j++)
if(costMat[i][j] != INF){
count++;
//fill edge list for the position 'count'
edgeList[count].u = i; edgeList[count].v = j;
edgeList[count].cost = costMat[i][j];
}
return count+1;
}
void sortEdge(edge *edgeList, int n){
//sort the edges of graph in ascending order of cost
int flag = 1, i, j;
for(i = 0; i<(n-1) && flag; i++){//modified bubble sort is used
flag = 0;
for(j = 0; j<(n-i-1); j++)
if(edgeList[j].cost > edgeList[j+1].cost){
swapping(edgeList[j], edgeList[j+1]);
flag = 1;
}
}
}
void kruskal(Tree &tr){
int ecount, maxEdge = V*(V-1)/2; //max n(n-1)/2 edges can have in a graph
edge edgeList[maxEdge], ed;
int uloc, vloc;
VSet VSetArray[V];
ecount = findEdge(edgeList);
for(int i = 0; i < V; i++)
VSetArray[i].addVertex(i);//each set contains one element
sortEdge(edgeList, ecount); //ecount number of edges in the graph
int count = 0;
while(count <= V-1){
ed = edgeList[count];
uloc = findVertex(VSetArray, ed.u);
vloc = findVertex(VSetArray, ed.v);
if(uloc != vloc){ //check whether source abd dest is in same set or not
merge(VSetArray[uloc], VSetArray[vloc]);
tr.addEdge(ed);
}
count++;
}
}
int main(){
Tree tr;
kruskal(tr);
tr.printEdges();
}输出
Edge: B--A And Cost: 1 Edge: E--B And Cost: 2 Edge: F--E And Cost: 2 Edge: C--A And Cost: 3 Edge: G--F And Cost: 3 Edge: D--A And Cost: 4 Total Cost: 15
更新时间：2020 年 6 月 11 日
1K+ 浏览
广告