数据结构中的最小生成树

**生成树**是无向图的一个子集，它通过最少的边将所有顶点连接起来。

如果图中所有顶点都连接，则至少存在一个生成树。在一个图中，可能存在多个生成树。

最小生成树

**最小生成树 (MST)** 是连接加权无向图中所有顶点的具有最小可能总边权重的边的子集。为了导出 MST，可以使用 Prim 算法或 Kruskal 算法。因此，我们将在本章中讨论 Prim 算法。

正如我们所讨论的，一个图可能有多个生成树。如果有 **n** 个顶点，则生成树应该有 **n - 1** 条边。在这种情况下，如果图的每条边都与权重相关联，并且存在多个生成树，我们需要找到图的最小生成树。

此外，如果存在任何重复的加权边，则图可能具有多个最小生成树。

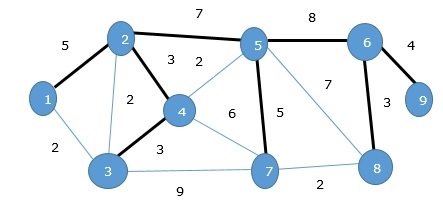
在上图中，我们展示了一个生成树，尽管它不是最小生成树。此生成树的成本为 (5 + 7 + 3 + 3 + 5 + 8 + 3 + 4) = 38。

更新于: 2019年8月27日

16K+ 浏览量

开启您的 职业生涯

通过完成课程获得认证

开始学习
广告