数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物
数学
英语
经济
心理学
社会学
时尚
法律数据结构中的二叉树遍历
在本章节，我们将看到不同的遍历算法，以遍历二叉查找树中存在的键。这些遍历是中序遍历、前序遍历、后序遍历和层次遍历。
假设我们有这样一棵树 −
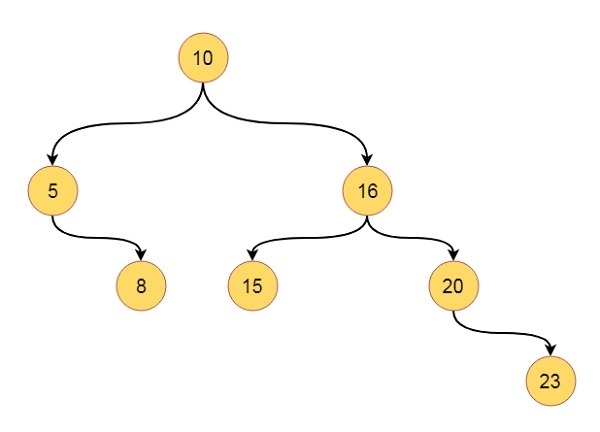
中序遍历序列将如下 − 5 8 10 15 16 20 23
前序遍历序列将如下 − 10 5 8 16 15 20 23
后序遍历序列将如下 − 8 5 15 23 20 16 10
层次遍历序列将如下 − 10, 5, 16, 8, 15, 20, 23
算法
inorderTraverse(root): Begin if root is not empty, then inorderTraversal(left of root) print the value of root inorderTraversal(right of root) end if End preorderTraverse(root): Begin if root is not empty, then print the value of root preorderTraversal(left of root) preorderTraversal(right of root) end if End postorderTraverse(root): Begin if root is not empty, then postorderTraversal(left of root) postorderTraversal(right of root) print the value of root end if End levelOrderTraverse(root): Begin define queue que to store nodes insert root into the que. while que is not empty, do item := item present at front position of queue print the value of item if left of the item is not null, then insert left of item into que end if if right of the item is not null, then insert right of item into que end if delete front element from que done End
示例
#include<iostream>
#include<queue>
using namespace std;
class node{
public:
int h_left, h_right, bf, value;
node *left, *right;
};
class tree{
private:
node *get_node(int key);
public:
node *root;
tree(){
root = NULL; //set root as NULL at the beginning
}
void inorder_traversal(node *r);
void preorder_traversal(node *r);
void postorder_traversal(node *r);
void levelorder_traversal(node *r);
node *insert_node(node *root, int key);
};
node *tree::get_node(int key){
node *new_node;
new_node = new node; //create a new node dynamically
new_node->h_left = 0; new_node->h_right = 0;
new_node->bf = 0;
new_node->value = key; //store the value from given key
new_node->left = NULL; new_node->right = NULL;
return new_node;
}
void tree::inorder_traversal(node *r){
if(r != NULL){ //When root is present, visit left - root - right
inorder_traversal(r->left);
cout << r->value << " ";
inorder_traversal(r->right);
}
}
void tree::preorder_traversal(node *r){
if(r != NULL){ //When root is present, visit left - root - right
cout << r->value << " ";
preorder_traversal(r->left);
preorder_traversal(r->right);
}
}
void tree::postorder_traversal(node *r){
if(r != NULL){ //When root is present, visit left - root - right
postorder_traversal(r->left);
postorder_traversal(r->right);
cout << r->value << " ";
}
}
void tree::levelorder_traversal(node *root){
queue <node*> que;
node *item;
que.push(root); //insert the root at first
while(!que.empty()){
item = que.front(); //get the element from the front end
cout << item->value << " ";
if(item->left != NULL) //When left child is present, insert into queue
que.push(item->left);
if(item->right != NULL) //When right child is present, insert into queue
que.push(item->right);
que.pop(); //remove the item from queue
}
}
node *tree::insert_node(node *root, int key){
if(root == NULL){
return (get_node(key)); //when tree is empty, create a node as root
}
if(key < root->value){ //when key is smaller than root value, go to the left
root->left = insert_node(root->left, key);
}else if(key > root->value){ //when key is greater than root value, go to the right
root->right = insert_node(root->right, key);
}
return root; //when key is already present, do not insert it again
}
main(){
node *root;
tree my_tree;
//Insert some keys into the tree.
my_tree.root = my_tree.insert_node(my_tree.root, 10);
my_tree.root = my_tree.insert_node(my_tree.root, 5);
my_tree.root = my_tree.insert_node(my_tree.root, 16);
my_tree.root = my_tree.insert_node(my_tree.root, 20);
my_tree.root = my_tree.insert_node(my_tree.root, 15);
my_tree.root = my_tree.insert_node(my_tree.root, 8);
my_tree.root = my_tree.insert_node(my_tree.root, 23);
cout << "In-Order Traversal: ";
my_tree.inorder_traversal(my_tree.root);
cout << "
Pre-Order Traversal: ";
my_tree.preorder_traversal(my_tree.root);
cout << "
Post-Order Traversal: ";
my_tree.postorder_traversal(my_tree.root);
cout << "
Level-Order Traversal: ";
my_tree.levelorder_traversal(my_tree.root);
}输出
In-Order Traversal: 5 8 10 15 16 20 23 Pre-Order Traversal: 10 5 8 16 15 20 23 Post-Order Traversal: 8 5 15 23 20 16 10 Level-Order Traversal: 10 5 16 8 15 20 23
更新于：2019-08-27
929 次阅读
广告