数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究从给定的中序和前序遍历构造树 (C++)
给定二叉树的中序和前序遍历，目标是从给定的遍历中构造一棵树。
中序遍历 - 在这种类型的树遍历中，先访问左子树，然后访问节点，最后访问右子树。
中序遍历（树根）
遍历根节点指向的左子树，调用中序遍历(root→left)
访问根节点
遍历根节点指向的右子树，调用中序遍历(root→right)
前序遍历 - 在这种类型的树遍历中，先访问节点，然后访问左子树，最后访问右子树。
前序遍历（树根）
- 访问根节点
- 遍历根节点指向的左子树，调用中序遍历(root→left)
- 遍历根节点指向的右子树，调用中序遍历(root→right)
下面给出了树的中序和前序遍历：
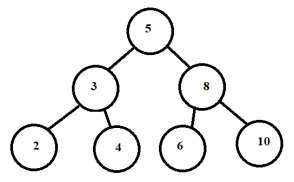
中序遍历
2-3-4-5-6-8-10
前序遍历
4-3-2-5-8-6-10
现在我们将根据给定的前序和中序遍历再次构造上面的树。
中序遍历
2-3-4-5-6-8-10
前序遍历
5-3-2-4-8-6-10
我们知道前序遍历首先访问根节点，因此第一个值始终表示树的根。从上面的序列中，5 是树的根。
前序遍历
5 -3-2-4-8-6-10
从上面的中序遍历中，我们知道节点的左子树在它之前被遍历，然后是它的右子树。因此，中序遍历中 5 左侧的所有值都属于它的左子树，右侧的所有值都属于它的右子树。
中序遍历
2-3-4 ← 5 → 6-8-10
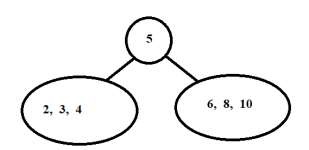
- 现在对左子树做同样的操作。
左子树的前序遍历是 3 - 2 - 4。所以 3 成为根。
中序遍历进一步细分为 2 ← 3 → 4
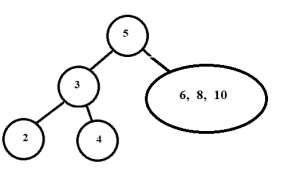
- 现在对右子树做同样的操作。
右子树的前序遍历是 8 - 6 - 10。所以 8 成为根。
中序遍历进一步细分为 6 ← 8 → 10
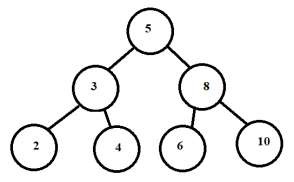
因此，通过这种方式，我们从给定的前序和中序遍历构造了原始树。
更新于：2020年8月3日
808 次浏览
广告