数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学数据结构中的二叉树ADT
基本概念
二叉树定义为：树中任何节点最多只有两个子节点。任何节点的最高度为二。这意味着二叉树的度为零、一或二。
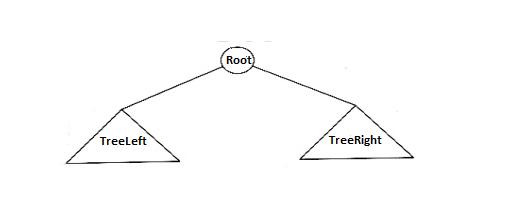
在上图中，二叉树由根节点和两个子树 TreeLeft 和 TreeRight 组成。二叉树左侧的所有节点都称为左子树，二叉树右侧的所有节点都称为右子树。
实现
二叉树最多有两个子节点；我们可以直接用指针指向它们。树节点的声明与双向链表的结构声明相同，即一个节点是一个结构体，包含关键信息加上指向其他节点的两个指针（左和右）。
二叉树节点声明
typedef struct tree_node *tree_ptr;
struct tree_node
{
element_type element1;
tree_ptr left1; tree_ptr right1;
};
typedef tree_ptr TREE;二叉树的类型
严格二叉树
严格二叉树定义为：所有节点都只有零个或两个子节点的二叉树。它不包含任何只有一个子节点的节点。
斜树
斜树定义为：除叶子节点外，每个节点只有一个子节点的二叉树。斜树有两种类型：左斜二叉树和右斜二叉树。
左斜二叉树
左斜树的节点只与左子节点相关联。它是一个只包含左子树的二叉树。
右斜二叉树
右斜树的节点只与右子节点相关联。它是一个只包含右子树的二叉树。
满二叉树或正则二叉树
如果所有叶子节点都在同一层，并且每个非叶子节点都恰好有两个子节点，并且它应该包含所有层中尽可能多的节点，则二叉树定义为满二叉树。高度为 h 的满二叉树最多有 2h+1 – 1 个节点。
完全二叉树
每个非叶子节点都恰好有两个子节点，但并非所有叶子节点都必须位于同一层。完全二叉树定义为：除最后一层外，所有层都具有最大数量的节点的二叉树。最后一层的元素应该从左到右填充。
几乎完全二叉树
几乎完全二叉树定义为：每个具有右子节点的节点也具有左子节点的树。具有左子节点的节点不需要具有右子节点。
一般树和二叉树的区别
一般树
- 一般树对子节点的数量没有限制。
- 在一般树中评估任何表达式都很困难。
二叉树
- 二叉树最多有两个子节点。
- 在二叉树中评估表达式很简单。
树的应用
- 算术表达式的操作
- 符号表的构造
- 语法分析
- 编写语法
- 表达式树的创建
更新于：2020年1月8日
9K+ 浏览量
广告