最小生成树与最短路径的区别

介绍

最小生成树和最短路径在图论领域设计网络方面起着至关重要的作用。虽然它们作为基本概念具有相似之处，但其目的却大相径庭。在本文中，我们将深入探讨图中这两个有趣的元素，并重点介绍它们的区别。最小生成树 (MST) 的目标是在所有顶点之间建立最小成本的连接，并且没有循环，而最短路径的目标是根据距离或权重累加来识别特定节点之间的最佳路径。

最小生成树与最短路径的区别

图论提供了各种工具，可以有效地分析网络中的连接和路径。虽然最小生成树和最短路径由于其对优化的关注而看起来相似，但它们在不同的场景中具有不同的用途。让我们来看一个简单的示例生成树图，

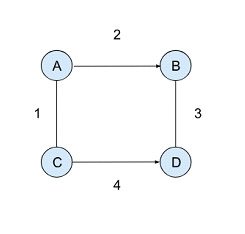
最小生成树

最小生成树定义为一个子图，它包含无向加权图的所有顶点，并且总边权重最小。构建 MST 的主要目标是在所有节点之间建立连接，同时最小化它们之间的总成本或距离。

为了创建 MST，可以使用克鲁斯卡尔算法或普里姆算法等各种算法。这些算法遍历每个顶点，直到使用具有最小可能权重的边连接每个节点，从而形成一个没有循环的树状结构。MST 的一个突出的现实生活应用在于通信网络（如电信或电力分配系统）；它有助于以最低成本建立有效的连接，通过消除可能导致资源和维护方面额外费用的不必要链接。

例如，让我们考虑一个简单的场景，我们旨在在一个城市中建立各个建筑物之间的电力连接。每个建筑物都由图中的一个节点表示，连接它们需要铺设电缆。为了最小化成本，我们使用克鲁斯卡尔算法或普里姆算法来识别最小生成树，它将代表连接所有建筑物最有效的网络设计，同时最大限度地减少电缆的使用。

最短路径

与专注于有效连接所有顶点同时最小化总权重的 MST 不同，最短路径算法根据长度或时间持续时间等指标识别两个特定顶点之间的最优路径。最短路径为我们提供了详细的导航说明，以便通过多个中间节点（如果需要）从 A 点到达 B 点。迪杰斯特拉算法是几种其他技术中的一个经典示例，它实际上反复探索不同的潜在路径，直到成功确定从起点到达特定目的地的最低累积成本或权重的路径。

最短路径的应用范围涵盖了各个领域，包括交通系统规划、为计算机网络设计的路由协议、确定最快路线的 GPS 导航应用程序、优化货物交付最有效路径的供应链优化解决方案，甚至社会网络分析测量分离度。

例如，假设我们正在使用手机上的 GPS 导航来查找从我们当前位置（节点 A）到所需目的地（节点 B）的最快速路线。此处使用的算法可能是迪杰斯特拉算法或贝尔曼-福特算法，它们根据道路长度或平均速度等因素计算最短路径。这些算法使我们能够确定到达目的地的最快方式，同时考虑沿途的任何中间停靠点或绕行。

最小生成树与最短路径的区别

结论

总而言之，尽管最小生成树和最短路径都涉及遍历图并在网络中识别最佳连接，但它们的目标在客观性和目的方面存在显著差异。虽然 MST 提供了一种经济的方式来实现整个图的组成元素之间的连接，但最短路径强调在网络中遍历特定道路时的效率——这使我们能够深入了解现实世界中旅行距离至关重要的场景。

Pranavnath

更新于：2023年8月25日

1K+ 次浏览

启动您的职业生涯

完成课程获得认证

开始学习