数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学数据结构中的范围树
范围树被定义为一种有序的树形数据结构，用于保存一系列点。它允许高效地检索给定范围内的所有点，通常在二维或更高维度中实现。它与kd树类似，但查询时间更快，为O(logd n + k)，但存储空间更差，为O(n logd-1 n)，其中d表示空间维度，n表示树中的点数，k表示给定查询检索到的点数。范围树可以与区间树区分开来：区间树不是存储点并允许高效检索给定范围内的点，而是存储区间并允许高效检索包含给定点的区间。
数据结构
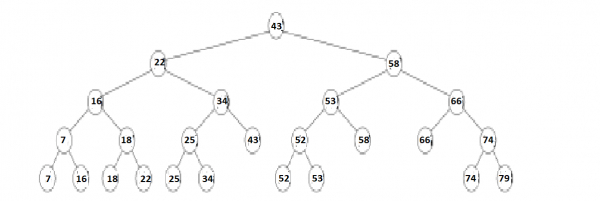
一维范围树示例。除叶子节点外，每个节点都存储其左子树中的最大值。
一组一维点上的范围树被视为这些点上的平衡二叉搜索树。存储在树中的点存储在树的叶节点中；每个内部节点存储其左子树中包含的最大值。一组d维点上的范围树是一个递归定义的多层二叉搜索树。数据结构的每一层都被视为d维中一个维度的二叉搜索树。第一层是d个坐标中第一个坐标的二叉搜索树。这棵树的每个顶点v都包含一个关联结构，该结构是v的子树中存储的点的最后(d−1)个坐标的(d−1)维范围树。
操作
构建
一组n个点的一维范围树是一个二叉搜索树，可以在O(n log n)时间内构建。更高维度的范围树是通过递归地构建点第一个坐标的平衡二叉搜索树来构建的，之后，对于这棵树中的每个顶点v，在v的子树中包含的点上构建一个(d−1)维范围树。这样构建范围树需要O(n logdn)时间。
更新于：2020年1月8日
3K+ 次浏览
广告