数据结构中的高度偏左树

在这里，我们将了解什么是高度平衡左倾树 (HBLT)。考虑一个二叉树，其中一个特殊的节点，称为**外部节点**，替换每个空子树。所有其他节点称为**内部节点**。当一些外部节点添加到某个二叉树中时，这称为**扩展二叉树**。

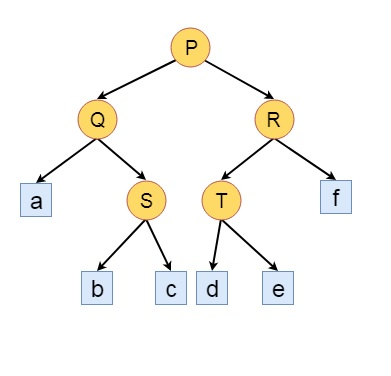
如果我们不考虑这棵树的叶子边，那么那就是实际的二叉树，而这是扩展的二叉树。

现在假设*s(x)*是从节点x到其子树中外部节点的最短路径的长度。如果x是外部节点，则其*s(x)*值为0。如果x是内部节点，则其值为：

min{𝑠(𝐿), 𝑠(𝑅)} + 1

这里L和R分别是x的左孩子和右孩子。现在让我们看看给定树的s值。

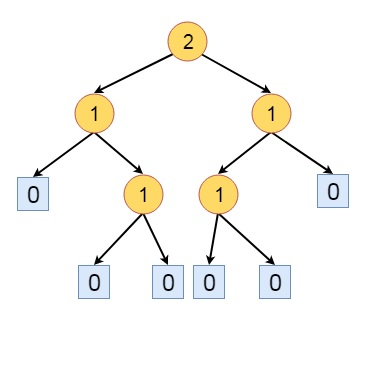
HBLT的定义如下：当且仅当每个内部节点的左孩子的s值大于或等于右孩子的s值时，二叉树才是高度平衡左倾树(HBLT)。

上图中的树不是HBLT。节点a的父节点具有s(L) = 0，而s(R)为1，除了所有其他节点都满足HBLT的规则。因此，如果我们调整该节点的左子树和右子树，使其成为HBLT。

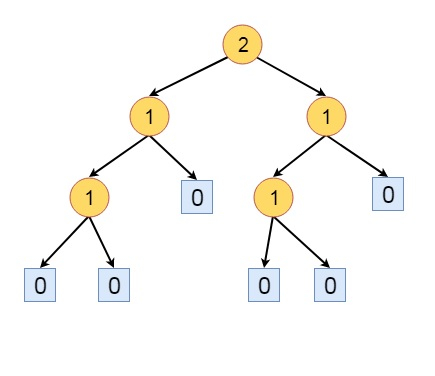
其他一些定义是：

• 最大树（最小树）是一棵树，其中每个节点的值都大于（小于）或等于其子节点。

• 最大HBLT是一个也是最大树的HBLT，最小HBLT是一个也是最小树的HBLT。

Arnab Chakraborty

更新于：2020年8月11日

1K+ 次浏览

开启您的职业生涯

通过完成课程获得认证

开始学习