扭转方程的推导

---

介绍

在固体力学领域，通过施加扭矩来扭曲材料的过程被称为扭转方程或扭转常数。扭转可以用多种方式表示，例如帕斯卡 (Pa)、牛顿米 (Nm) 或英尺磅力 (ft·lbf)。扭转常数的 SI 单位是牛顿每平方米 (N/m²) 或磅每平方英寸 (psi)。

对于非圆形截面，在发生扭曲的同时也会发生翘曲变形。在翘曲过程中，横截面变得不规则。扭转方程也称为扭转常数。在纯扭转方程的推导中，必须遵循胡克定律以及其他条件。

对于圆形截面，必须保持其圆形形状。此处，颗粒的应力永不超过其弹性极限。横截面的面积必须保持平面。

什么是扭转？

图1：扭转

在固体力学中，扭转是指由于施加扭矩而导致特定物体扭曲的特性。扭转可以用帕斯卡 (Pa) 或牛顿每平方米 (N/m²) 的 SI 单位来描述，也可以用磅每平方英寸 (psi) 来表示。

然而，与之相反的是，扭矩用牛顿米 (Nm) 或英尺磅力表示。给定物体中的某些截面垂直于作用扭矩轴。在这些特定位置，合剪应力垂直于半径。在形状不规则的横截面中，会发生扭曲以及翘曲变形；这种特殊的变形称为翘曲。在翘曲处，横截面粗糙。

扭转常数

扭转常数与杆横截面的几何特性有关，该特性与通过杆轴的施加扭矩以及由扭转形成的角度有关。所有这些特定理论都与均匀的塑性杆有关。正如 Atavin 等人 (2018) 所述，杆的抗扭刚度由扭转常数决定，该常数与物体的不同特性（例如长度）相结合。扭转常数的 SI 单位用 m⁴ 表示。

扭转方程推导

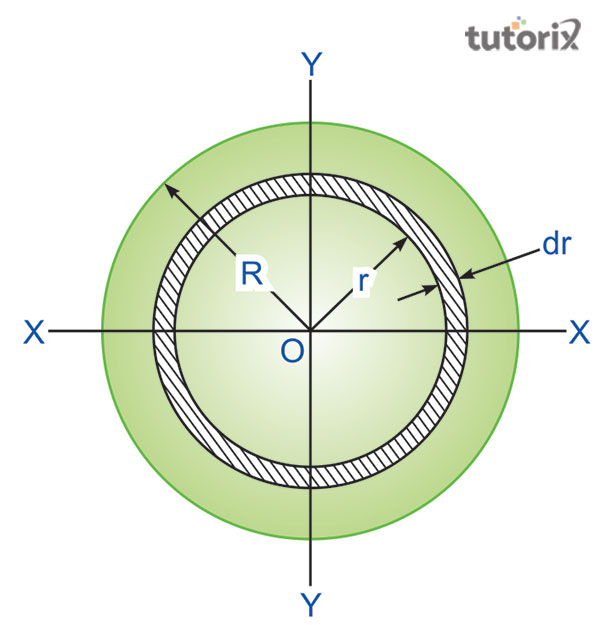
图2：圆形轴的扭转方程

考虑一个具有指定半径 R 的实心圆形轴，它与作用在其两端相同扭矩 T 的扭矩相关 (hkdivedi，2022)。

$\mathrm{半径角度=\frac{弧长}{半径}}$

$\mathrm{弧长 AB = R\theta = L\gamma }$

$\mathrm{\gamma =\frac{R\theta }{L}}$

此处，与圆形轴相关的两个不同的固定点为 A 和 B

并且，γ 是 AB 形成的角度

刚度模量用 $\mathrm{G=\frac{\tau }{\gamma } }$ 表示

此处，剪应力用 𝜏 表示，剪应变用 γ 表示

$\mathrm{\frac{\tau }{G}=\Gamma }$

因此可以确定 $\mathrm{\frac{R\theta }{L}=\frac{\tau }{G} }$

考虑一个半径为 r、厚度为 dr 的小条带，它承受剪应力。

$\mathrm{\Gamma'*2\pi rdr}$

此处，r 是小条带的半径

条带的厚度用 dr 表示

剪应力为 γ

轴中心的扭矩 $\mathrm{2\pi\, \Gamma'\, r^{2}dr}$

$\mathrm{T=\int_{0}^{R}2\pi\, \Gamma'\, r^{2}dr}$

$\mathrm{T=\int_{0}^{R}2\pi\, \frac{G\theta }{L}\, r^{3}dr}$

$\mathrm{T=\frac{2\pi\,G\theta }{L}\int_{0}^{R}r^{3}dr=\frac{G\theta }{L}\left [ \frac{\pi d^{4}}{32} \right ]}$

代入并积分 R 的值

$\mathrm{\frac{G\theta }{L}J}$

因此，对极惯性矩进行代换得到：

$\mathrm{\frac{T }{J}=\frac{\tau }{r}=\frac{G\theta }{L}}$

扭转方程的假设

• 材料具有弹性 (Engineeringtoolbox，2022)。

• 物体需要遵守胡克定律

• 剪应力必须与剪应变成比例

• 横截面的面积需要是平面的。

• 圆形截面需要保持圆形

• 材料的直径需要旋转一定角度

• 材料中存在的应力不应高于弹性极限

这些是材料为了获得所需结果而需要遵循的假设。

结论

扭转方程主要遵循胡克定律，贯穿其整个推导过程。此处使用的材料本质上是均匀的，这意味着它们具有弹性。为了推导出正确的扭转方程，可以遵循的主要假设之一是，颗粒中的剪应力必须与剪应变成比例。此处的一些截面垂直于扭矩轴。合剪应力也垂直于半径。关于轴中的剪应力，可以提到，如果轴承受扭矩和扭曲，则会形成剪应力。

常见问题

Q1. 扭转常数是什么意思？

A1. 扭转常数是指与杆轴相关的横截面杆的几何特性。在这种情况下，施加的扭矩和扭曲角之间存在联系，其 SI 单位为：m⁴。

Q2. 扭矩的概念是什么？

A2. 在力学中，扭矩是指在旋转运动中产生的力。扭矩也称为旋转力、力矩和转动效应。

Q3. 扭转方程推导的假设是什么？

A3. 扭转方程推导的假设包括：它在整个方程推导过程中遵循胡克定律。扭转中使用的材料必须具有与剪应变成比例的剪应力。圆形截面必须保持圆形，并且材料的应力不得超过弹性极限。

Q4. 扭转是什么意思？

A4. 通过施加任何特定力来扭曲和扭转物体被称为扭转。扭曲的状态和扭曲的性质是扭转的两个最重要的部分。