数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学麦克斯韦-玻尔兹曼分布推导
引言
在热力学和统计力学中，我们经常研究容器内的气体分子。在这种情况下，不可能单独研究每个分子。事实上，即使在一毫升的气体中，也有几乎无数的气体分子。因此，我们不研究单个分子，而是将其作为一个系统来研究。
当我们处理系统时，我们会通过选择一定范围的速度并试图找出以该速度运动的分子数量来描述它们。这就是麦克斯韦-玻尔兹曼分布派上用场的地方。
什么是宏观态？
要理解这个术语，你应该理解什么是宏观性质。宏观性质是系统可以用肉眼看到和观察到的性质。例如，系统的温度、压力和体积是宏观变量。
因此，宏观态是指在这些性质的背景下系统的状态。例如，说一个系统处于300K的温度，这是一个关于其宏观态的陈述。系统如何达到这个温度，或者内部各个分子的温度是多少，这并不重要。系统本身处于300K，就是这样。
在统计力学中，宏观态是一组能量值、粒子数和体积值，这些值表征了一个系统。
另一个例子是抛硬币两次。你可能有以下结果：
正面-正面
正面-反面
反面-正面
反面-反面
人们可以说一个正面和一个反面是一个宏观态。硬币在什么时候落在正面，什么时候落在反面并不重要；重要的是有一个正面和一个反面。
什么是微观态？
与宏观态相反，微观态是指系统根据其微观性质是如何组织的。例如，要获得一瓶300K的水，你可以将等量的290K的热水和310K的冷水混合在一起。或者你可以将不同数量的不同温度的水混合在一起以获得相同的结果。达到特定宏观态的不同方法中的每一种都称为微观态。
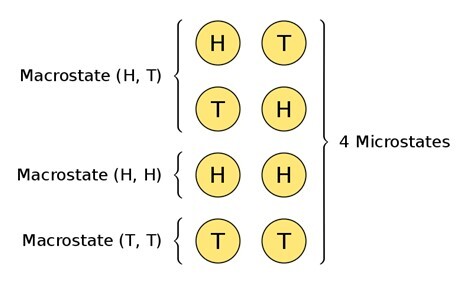
在抛硬币两次的例子中，一个正面和一个反面是一个宏观态，其特征是两种可能的微观态：H-T或T-H。在统计力学中，微观态是特定系统达到特定宏观态的许多可能方式之一。
麦克斯韦-玻尔兹曼分布定律
当你拿一个装满任何气体的容器时，气体分子在容器内并不是静止的。相反，它们在不同的方向上以不同的速度随机移动。事实上，正是这种运动导致了气体的压力。由于不可能描述每个粒子的确切速度，我们使用所谓的麦克斯韦-玻尔兹曼分布定律。
简单地说，该定律描述了速度在v到v+dv范围内的粒子的分数。数学上，该定律表示为：
$$\mathrm{F\:(v)\:d^{3}v\:=\:(\frac{m}{2\Pi\:KT})^{3/2}\:e^{-\:\frac{mv^{2}}{2KT}}\:d^{3}\:v}$$
这里，𝑓(𝑣)𝑑³𝑣表示速度在v到v+dv范围内的粒子分数。
麦克斯韦分布定律的推导
考虑一个体积为V的容器中含有n个粒子的系统。设可能的能级由𝜖₁, 𝜖₂, … , 𝜖ᵣ表示。具有能量𝜖ᵢ的粒子数用𝑛ᵢ表示。
然后，达到特定微观态的方式数量使用以下公式给出：
$$\mathrm{W\:=\:\frac{n!}{n_{1}!\times\:n_{2}!\times\:n_{3}!.......\:n_{r}!}}$$
这个公式可能难以使用，我们取它的自然对数来去除分数。此外，我们应用斯特林近似。然后，
$$\mathrm{ln\:ln\:W\:=\:ln\:ln\:n!\:-\:ln\:ln\:({n_{1}!\times\:n_{2}!\times\:n_{3}!.......\:n_{r}!})\:ln\:ln\:(n!)\:=\:n\:ln\:ln\:(n)-\:n\:ln\:ln\:W\:=\:n\:ln\:ln\:(n)\:-\:n\:-\:\displaystyle\sum\limits_{i=0}^r (n_{1}\:ln\:ln\:(n)\:-\:n_{i}}$$
我们需要最大化W的值。为此，我们对上述等式求微分并将其设为零。由于n是常数，我们得到：
$\mathrm{\partial\:ln\:ln\:W\:=\:-\:\displaystyle\sum\limits_{i=0}^r (\partial\:n_{i}\:ln\:ln\:(n_{i}))+n_{i}\times\:\frac{1}{n_{i}}\:-\:\partial\:n_{i}\:=\:0}$ 因此，$\mathrm{\displaystyle\sum\limits_{i=0}^r (\partial\:n_{i}\:ln\:ln\:(n_{i}))\:=\:0}$
现在，当n为常数时，和$\mathrm{\displaystyle\sum\limits^r\:n_{i}\:=\:n}$ 因此，
$$\mathrm{\displaystyle\sum\limits_{i}^r\partial\:n_{i}\:=\:0}$$
此外，由于总能量是常数，
$$\mathrm{\displaystyle\sum\limits_{i}^r\varepsilon\:_{i}\partial\:n_{i}\:=\:0}$$
我们现在使用拉格朗日未定乘子法得到
$$\mathrm{\displaystyle\sum\limits_{i}^r(Ln\:ln\:n_{i}\:+\:\alpha\:+\:\beta\:\varepsilon\:_{i})\:\partial\:n_{i}\:=\:0}$$
为了使上述等式成立，括号中的项必须分别为零。这只在以下情况下成立：
$$\mathrm{n_{i}\:=\:e^{-\alpha}\:\times\:e^{-\beta\:\varepsilon_{i}}}$$
这与上面给出的麦克斯韦-玻尔兹曼分布的形式相似，因为能量与速度的平方成正比。常数的值是一个较长的推导，无法在一篇文章中容纳。
应用
计算平均速度、最可能速度和均方根速度。
利用麦克斯韦-玻尔兹曼分布，可以推导出粒子的平均速度、分子最有可能具有的速度以及分子的均方根速度的值。这些是描述系统的重要参数。
计算能量
与系统相关的平均能量以及每个粒子的平均能量可以从我们推导出的分布函数中计算出来。事实上，结果与通过其他方法进行的推导非常吻合。
结论
系统的宏观态是指其根据宏观性质（如温度和压力等）的配置。从统计学上讲，它是一组能量、粒子数和系统的体积。
麦克斯韦-玻尔兹曼分布可以给出速度在v到v+dv范围内的分子分数。它是由詹姆斯·克拉克·麦克斯韦在启发式基础上给出的，而玻尔兹曼后来研究了它的物理解释。分布函数如下：
$$\mathrm{F\:(v)\:d^{3}v\:=\:(\frac{m}{2\Pi\:KT})^{3/2}\:e^{-\:\frac{mv^{2}}{2KT}}\:d^{3}\:v}$$
常见问题
1. 我见过麦克斯韦分布定律、麦克斯韦-玻尔兹曼分布、麦克斯韦分布等多个名称。它们是相同的，还是只有一个特定的名称是正确的？
所有这些术语都指同一定律：麦克斯韦-玻尔兹曼分布定律。使用一个特定的名称而不是另一个名称没有任何惩罚。由于玻尔兹曼也对这个定律做出了重大贡献，所以它最常被称为完整名称。
2. 麦克斯韦分布能否用速度以外的参数表示？
是的。气体分子的速度决定了它的能量和压力。有时，分布函数是用能量而不是速度表示的。这不会改变定律的性质。
3. 麦克斯韦分布在量子力学上是否有效？
只有当量子效应不显著时，麦克斯韦-玻尔兹曼分布才成立。
4. 推导麦克斯韦分布有多种方法吗？
是的。没有推导该定律的严格证明。有多种方法可以推导出它，每种方法都有其自身的优点和缺点。人们甚至可以不谈论微观态和宏观态就推导出它。
5. 麦克斯韦分布的图形是什么样的？
该图在一个特定值处有一个峰值，而在该值的任一侧则衰减。该图随温度而变化。
浏览量：205
